题目内容
12．如果a=log41，b=log23，c=log2π，那么三个数的大小关系是（ ）| A． | c＞b＞a | B． | a＞c＞b | C． | a＞b＞c | D． | b＞c＞a |
分析 利用对数函数的单调性即可得出．
解答 解：∵a=log41=0，1＜b=log23＜c=log2π，
∴c＞b＞a．
故选：A．
点评 本题考查了对数函数的单调性，考查了推理能力与计算能力，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
2．已知向量$\overrightarrow{OA}=（3，1）$，$\overrightarrow{OB}=（-1，3）$，$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}$（m＞0，n＞0），若m+n∈[1，2]，则$|\overrightarrow{OC}|$的取值范围是（ ）
| A． | $[\sqrt{5}，2\sqrt{5}]$ | B． | $[\sqrt{5}，2\sqrt{10}）$ | C． | $（\sqrt{5}，\sqrt{10}）$ | D． | $[\sqrt{5}，2\sqrt{10}]$ |
3．已知集合A={x|x=3n+2，n∈N}，B={6，8，10，12，14}，则集合A∩B=（ ）
| A． | {8，10} | B． | {8，12} | C． | {8，14} | D． | {8，10，14} |
4．定积分$\int_{1}^{3}{（2x-\frac{1}{x}）}\;dx$=（ ）
| A． | 10-ln3 | B． | 8-ln3 | C． | $\frac{22}{3}$ | D． | $\frac{64}{9}$ |
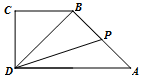如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，P是AB的中点，则$\overrightarrow{DP}•\overrightarrow{AB}$=-1．