题目内容
已知P为抛物线y=x2上的动点,定点A(a,0)关于P点的对称点是Q.求点Q的轨迹方程.
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出P,Q两点的坐标,根据定点A(a,0)关于P点的对称点是Q,写出中点的坐标公式,用a,x表示x0,y0,根据P是曲线上的一点,代入曲线的方程,得到要求的点的轨迹.
解答:
解:设Q(x,y)、P(x0,y0)
∵定点A(a,0)关于P点的对称点是Q,
∴x0=
,y0=
,
∵P为抛物线y=x2上的动点,
∴y0=x02,
∴
=(
)2,即y=
(x+a)2,
∴点Q的轨迹方程为y=
(x+a)2.
∵定点A(a,0)关于P点的对称点是Q,
∴x0=
| x+a |
| 2 |
| y |
| 2 |
∵P为抛物线y=x2上的动点,
∴y0=x02,
∴
| y |
| 2 |
| x+a |
| 2 |
| 1 |
| 2 |
∴点Q的轨迹方程为y=
| 1 |
| 2 |
点评:本题考查轨迹方程,考查代入法,确定坐标之间的关系是关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
函数f(x)=log(x-1)+2(a>0且a≠1)的图象恒过定点为( )
| A、(3,2) |
| B、(2,1) |
| C、(2,2) |
| D、(2,0) |
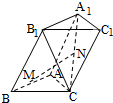 如图,已知三棱柱ABC-A1B1C1.
如图,已知三棱柱ABC-A1B1C1.