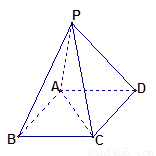
题目内容
已知四棱锥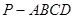 的底面
的底面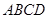 是边长为
是边长为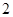 的正方形,
的正方形,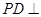 底面
底面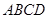 ,
,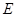 、
、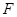 分别为棱
分别为棱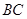 、
、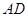 的中点.
的中点.
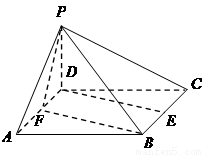
(1)求证: 平面
平面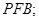
(2)已知二面角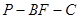 的余弦值为
的余弦值为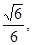 求四棱锥
求四棱锥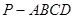 的体积.
的体积.
【答案】
(1)证明:因为 分别为正方形
分别为正方形 的两边
的两边 的中点,
的中点,
所以 即
即 为平行四边形,
为平行四边形, 分
分
 分
分
 平面
平面 且
且 平面
平面
 平面
平面 分
分
(2)以 为原点,直线
为原点,直线 分别为
分别为 轴建立空间直角坐标系.设
轴建立空间直角坐标系.设
 可得如下点的坐标:
可得如下点的坐标:
则有 分
分
因为 底面
底面 所以平面
所以平面 的一个法向量为
的一个法向量为 分
分
设平面 的一个法向量为
的一个法向量为 则可得
则可得 即
即
令 得
得 所以
所以 分
分
由已知,二面角 的余弦值为
的余弦值为 所以得
所以得
 分
分

【解析】略

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点 分别是
分别是 的中点.求
的中点.求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);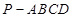 的底面
的底面 是边长为4的正方形,
是边长为4的正方形,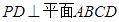 ,
,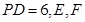 分别为
分别为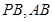 中点。
中点。 。
。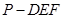 的体积。
的体积。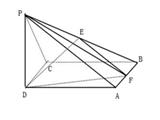
 的底面是边长为2的正方形,
的底面是边长为2的正方形,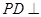 面
面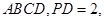
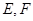 分别为
分别为 的中点.[来源:学.科.网Z.X.X.K]
的中点.[来源:学.科.网Z.X.X.K] 与面
与面 所成的角;
所成的角; 的大小.
的大小.
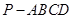 的底面是边长为2的正方形,
的底面是边长为2的正方形,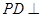
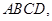
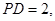
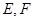 分别为
分别为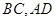 的中点,
的中点,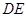 与面
与面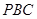 所成角的正弦值;
所成角的正弦值;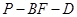 的正切值.
的正切值.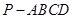 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且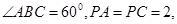
 .
.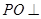 平面
平面 ;
; 是
是 的中点,求异面直线
的中点,求异面直线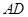 与
与 所成角的余弦值.
所成角的余弦值.