题目内容
10.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的交点在x轴上的射影恰为该椭圆的焦点,则双曲线的离心率为$\frac{\sqrt{13}}{2}$.分析 设渐近线y=$\frac{b}{a}$x与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1交于A(x1,y1),B(-x1,-y1)两点,由题意求得A点坐标,代入渐近线方程,求得$\frac{b}{a}$=$\frac{3}{2}$,根据双曲线的离心率公式率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,即可求得双曲线的离心率.
解答 解:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的焦点坐标为(±1,0),
设渐近线y=$\frac{b}{a}$x与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1交于A(x1,y1),B(-x1,-y1)两点,
则x1=1,解得:y1=$\frac{3}{2}$,则A(1,$\frac{3}{2}$),
代入渐近线方程整理得:$\frac{b}{a}$=$\frac{3}{2}$,
双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{13}}{2}$,
故答案为:$\frac{\sqrt{13}}{2}$.
点评 本题考查椭圆的简单几何性质,考查双曲线的离心率公式及渐近线方程,考查计算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
4.已知集合A={x|(x+2)(x-3)≤0,x∈Z},B={x|(x+1)(x-1)(x-3)=0},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
15.执行右面的程序框图,如果输出的a值大于2017,那么判断框内的条件为( )

| A. | k<9? | B. | k≥9? | C. | k<10? | D. | k≥11? |
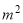 的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1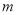 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 ,那么下面不等式一定成立的是( )
,那么下面不等式一定成立的是( ) B.
B. C.
C. D.
D.