题目内容
已知抛物线的焦点在x轴上,直线y=2x-4被抛物线截得的线段长为 ,则抛物线的标准方程是 .
,则抛物线的标准方程是 .
【答案】分析:设出抛物线方程y2=2px,联立方程组,通过弦长公式,求出抛物线中的变量p,求出抛物线方程.
解答:解:设抛物线方程为:y2=2px,
所以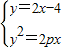 ,
,
可得2x2-(8+p)x+8=0,
由韦达定理可知:x1+x2=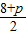 ,x1x2=4.
,x1x2=4.
直线y=2x-4被抛物线截得的线段长为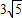 =
=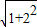 |x2-x1|=
|x2-x1|=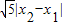 ,
,
即:9=(x1+x2)2-4x1x2,9=(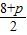 )2-4×4,
)2-4×4,
解得p=2或p=-18.
抛物线标准方程为:y2=4x或y2=-36x.
故答案为:y2=4x或y2=-36x.
点评:本题考查求抛物线方程,利用弦长公式,是解题的关键,考查计算能力,常考题型.
解答:解:设抛物线方程为:y2=2px,
所以
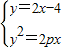 ,
,可得2x2-(8+p)x+8=0,
由韦达定理可知:x1+x2=
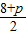 ,x1x2=4.
,x1x2=4.直线y=2x-4被抛物线截得的线段长为
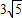 =
=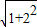 |x2-x1|=
|x2-x1|=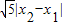 ,
,即:9=(x1+x2)2-4x1x2,9=(
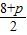 )2-4×4,
)2-4×4,解得p=2或p=-18.
抛物线标准方程为:y2=4x或y2=-36x.
故答案为:y2=4x或y2=-36x.
点评:本题考查求抛物线方程,利用弦长公式,是解题的关键,考查计算能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目