题目内容
已知函数 在
在 处取得极小值.
处取得极小值.
(1)求 的值;
的值;
(2)若 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线 不可能在直线
不可能在直线 的下方.
的下方.
(1)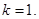 (2)证明当
(2)证明当 时,曲线
时,曲线 不可能在直线
不可能在直线 的下方.那么只要证明存在一个变量函数值大于函数
的下方.那么只要证明存在一个变量函数值大于函数 的函数值,即可。
的函数值,即可。
解析试题分析:解:(1)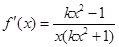 ,由已知得
,由已知得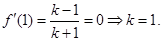 3分
3分
当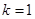 时
时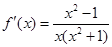 ,此时
,此时 在
在 单调递减,在
单调递减,在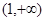 单调递增 5分
单调递增 5分
A. 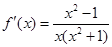 ,
,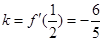 ,
, 在
在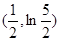 的切线方程为
的切线方程为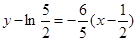 ,即
,即 8分
8分
当 时,曲线
时,曲线 不可能在直线
不可能在直线 的下方
的下方
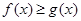 在
在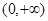 恒成立,令
恒成立,令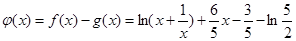 ,
,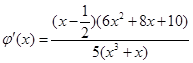
当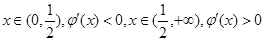 ,
,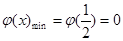 ,即
,即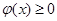
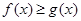 在
在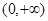 恒成立,所以当
恒成立,所以当 时,曲线
时,曲线 不可能在直线
不可能在直线 的下方 13分
的下方 13分
考点:导数的运用
点评:主要是考查了导数的运用,研究函数的单调性,以及函数的最值,属于中档题。

练习册系列答案
相关题目
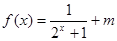 ,
,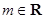 .
.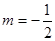 ,求证:函数
,求证:函数 是
是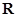 上的奇函数;
上的奇函数;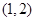 上没有零点,求实数
上没有零点,求实数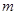 的取值范围.
的取值范围.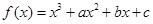 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.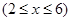 .
.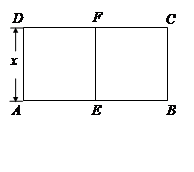
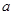 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
 ;
; 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围. .
.  ;
; 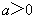 ,求证:
,求证: ≤
≤ .
.
