题目内容

6．已知a∈R，函数f（x）=x3-ax2+ax+a，g（x）=f（x）+（a-3）x．
（1）求证：曲线y=f（x）在点（1，f（1））处的切线过点（2，4）；
（2）若g（1）是g（x）在区间（0，3]上的极大值，但不是最大值，求实数a的取值范围．

分析 （1）求出函数的导数，计算f′（1），f（1），求出求出方程，从而求出定点即可；
（2）求出g（x）的导数，根据g（1）是g（x）在区间（0，3]上的极大值，不是最大值，得到关于a的不等式，解出即可．

解答 （1）证明：∵f'（x）=3x2-2ax+a，∴f'（1）=3-a，
∵f（1）=a+1，∴曲线y=f（x）在点（1，f（1））处的切线方程为y-（a+1）=（3-a）（x-1），
即a（x-2）=3x-y-2，令x=2，则y=4，
故曲线y=f（x）在点（1，f（1））处的切线过定点（2，4）；
（2）解：g'（x）=f'（x）+a-3=3x2-2ax+2a-3=（x-1）[3x-（2a-3）]，
令g'（x）=0得x=1或x=$\frac{2a-3}{3}$，
∵g（1）是g（x）在区间（0，3]上的极大值，
∴$\frac{2a-3}{3}$＞1，∴a＞3，
令g'（x）＞0，得x＜1或x＞$\frac{2a-3}{3}$，g（x）递增；
令g'（x）＜0，得1＜x＜$\frac{2a-3}{3}$，g（x）递减，
∵g（1）不是g（x）在区间（0，3]上的最大值，
∴g（x）在区间（0，3]上的最大值为g（3）=18-2a，
∴g（3）=18-2a＞g（1）=2a-2，∴a＜5，又a＞3，
∴3＜a＜5．

点评 本题考查了函数的单调性、极值、最值问题，考查导数的应用，是一道中档题．

练习册系列答案
相关题目
14．已知函数f（x）=x2+ax+b（a，b∈R），记集合A={x∈R|f（x）≤0}，B={x∈R|f（f（x）+1）≤0}，若A=B≠∅，则实数a的取值范围为（　　）
A．[-4，4]B．[-2，2]C．[-2，0]D．[0，4]
15．如图，矩形ABCD中，$AB=2\sqrt{2}$，$AD=\sqrt{2}$，M为DC的中点，将△DAM沿AM折到△D′AM的位置，AD′⊥BM．
（1）求证：平面D′AM⊥平面ABCM；
（2）若E为D′B的中点，求三棱锥A-D′EM的体积．
14．下列函数在区间[0，+∞）上是增函数的是（　　）
①y=2x　②y=x2+2x-1　③y=|x+2|④y=|x|+2．
A．①②B．①③C．②③④D．①②③④
1．已知数列{an}的前n项和Sn=$\frac{{n}^{2}+3n}{4}$，n∈N*．
（1）求数列{an}的通项公式；
（2）设bn=（n+1）4${\;}^{{a}_{n}}$-$\frac{1}{4{a}_{n}{a}_{n+1}}$，求数列{bn}的前n项和．
11．已知函数f（x）=|lnx|，g（x）=k（x-1）（k∈R）．
（1）若两个实数a，b满足0＜a＜b，且f（a）=f（b），求4a-b的取值范围；
（2）证明：当k＜1时，存在x0＞1，使得对任意的x∈（1，x0），恒有f（x）＞g（x）；
（3）已知0＜a＜b，证明：存在x0∈（a，b），使得$\frac{lnb-lna}{b-a}=\frac{1}{x_0}$．
18．极坐标系与直角坐标系xOy有相同的长度单位，以原点为极点，以x轴正半轴为极轴，曲线C1的极坐标方程为ρ=4sinθ，曲线C2的参数方程为$\left\{{\begin{array}{l}{x=m+tcosα}\\{y=tsinα}\end{array}}\right.$（t为参数，0≤α＜π），射线$θ=φ，θ=φ+\frac{π}{4}，θ=φ-\frac{π}{4}$与曲线C1交于（不包括极点O）三点A，B，C．
（1）求证：$|{OB}|+|{OC}|=\sqrt{2}|{OA}|$；
（2）当$φ=\frac{5π}{12}$时，B，C两点在曲线C2上，求m与α的值．
15．执行如图程序框图（见上图），如果输入的x，t均为2，S=（　　）
A．7B．6C．5D．4
16．执行如图所示的程序框图，则输出的b值等于（　　）
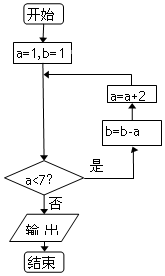
A．-24B．-15C．-8D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网