题目内容
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]()
![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.
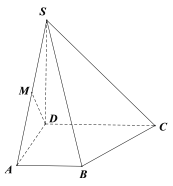
(Ⅰ)证明:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 平面
平面![]() . 若存在,确定
. 若存在,确定![]() 点的位置;若不存在,说明理由.
点的位置;若不存在,说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)![]() ;(Ⅲ)见解析
;(Ⅲ)见解析
【解析】
(I)依题意易得![]() 两两垂直,以
两两垂直,以![]() 为原点建立空间直角坐标系.通过
为原点建立空间直角坐标系.通过![]() ,
,![]() 证得
证得![]() 平面
平面![]() .(II)通过计算平面
.(II)通过计算平面![]() 和平面
和平面![]() 的法向量,由此计算出面面角的余弦值,进而求得二面角的大小.(III)设出
的法向量,由此计算出面面角的余弦值,进而求得二面角的大小.(III)设出![]() 的坐标,利用直线
的坐标,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量垂直,求出关于
的法向量垂直,求出关于![]() 点坐标的参数,由此判断出
点坐标的参数,由此判断出![]() 点的位置.
点的位置.
(Ⅰ)因为![]()
![]() 平面
平面![]() .
.
所以![]() ,
,![]() ,又
,又![]() .
.
如图,以![]() 为原点建立空间直角坐标系.
为原点建立空间直角坐标系.
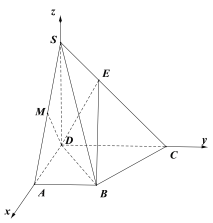
由题意得![]()
所以![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() .
.
所以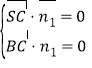 ,即
,即![]() ,
,
令![]() ,则
,则![]() .
.
于是![]() .
.
因为![]() ⊥平面
⊥平面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
又![]() .
.
所以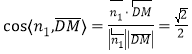 .
.
因为所求二面角为钝角,所以二面角![]() 大小为
大小为![]() .
.
(Ⅲ)解:设![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则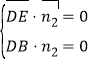 ,即
,即 ![]() ,
,
令![]() ,
,![]() ,
,![]() . 于是
. 于是![]() ,
,
如果直线![]() 平面
平面![]() ,
,
那么![]() ,解得
,解得 ![]() .
.
所以,存在点![]() 为线段
为线段![]() 靠近
靠近![]() 点的三等分点,使得直线
点的三等分点,使得直线![]() 平面
平面![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度![]() (单位:cm)的情况如表1:
(单位:cm)的情况如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年11月份AQI指数频数分布如表2:
|
|
|
|
|
|
频数(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)设
(2)小李在该市开了一家洗车店,洗车店每天的平均收入与AQI指数存在相关关系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根据表3估计小李的洗车店2017年11月份每天的平均收入.
附参考公式:![]() ,其中
,其中 ,
,![]() .
.


