题目内容
4.正方体ABCD-A1B1C1D1中,棱长为$\sqrt{3}$,各面上到A点距离为2的点所围成的封闭曲线的长度是$\frac{5π}{2}$.分析 正方体的各个面根据与球心位置关系分成两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,各弧圆心角为$\frac{π}{6}$,A1B1C1D1、B1BCC1、D1DCC1为与球心距离为1的截面,截痕为小圆弧,由于截面圆半径为r=1,故各段弧圆心角为$\frac{π}{2}$这条曲线长度为3•$\frac{π}{6}$•2+3•$\frac{π}{2}$?•=$\frac{5π}{2}$.
解答 解:由题意,此问题的实质是以A为球心、2为半径的球在正方体ABCD-A1B1C1D1各个面上交线的长度计算,
正方体的各个面根据与球心位置关系分成两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,
由AB=$\sqrt{3}$,AE=2,cos∠EAB=$\frac{AB}{AE}$=$\frac{\sqrt{3}}{2}$,
∴∠DAF=∠EAB=$\frac{π}{6}$,
则∠FAE=$\frac{π}{6}$,
同理可知:各弧圆心角为$\frac{π}{6}$,
A1B1C1D1、B1BCC1、D1DCC1为与球心距离为1的截面,截痕为小圆弧,
由于截面圆半径为r=1,故各段弧圆心角为$\frac{π}{2}$
∴这条曲线长度为3•$\frac{π}{6}$•2+3•$\frac{π}{2}$•=$\frac{5π}{2}$,
故答案为:$\frac{5π}{2}$.
点评 本题考查点到直线距离公式的应用,考查空间想象能力,属于中档题.

练习册系列答案
相关题目
9.若函数y=log3x的反函数为y=g(x),则$g(\frac{1}{2})$的值是( )
| A. | 3 | B. | ${log_3}\frac{1}{2}$ | C. | log32 | D. | $\sqrt{3}$ |
16.sin2010°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
13.已知$\overrightarrow{e_1},\overrightarrow{e_2}$是两个不共线的向量,且$\overrightarrow a=\overrightarrow{e_1}+m\overrightarrow{e_2}$与$\overrightarrow b=-3\overrightarrow{e_1}-\overrightarrow{e_2}$共线,则m=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
14.命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则下列正确的是( )
| A. | p∨q为真 | B. | p∧q为真 | C. | p∨q为假 | D. | q为真 |
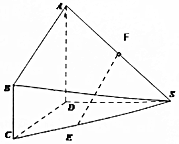 如图,在几何体SABCD中,AD⊥平面SCD,BC∥AD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,F是SA的中点,E在SC上,AE=$\sqrt{5}$.
如图,在几何体SABCD中,AD⊥平面SCD,BC∥AD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,F是SA的中点,E在SC上,AE=$\sqrt{5}$.