题目内容
8．是否存在这样的实数a，使得函数f（x）=x2+（3a-2）x+a-1图象在区间（-1，3）上与x轴有且只有一个交点？若存在，求出a的取值范围；若不存在，请说明理由．分析 此题考查的是函数与方程的综合应用类问题．在解答时，先结合存在性问题的特点先假设存在a符合题意，然后将问题转化为函数零点存在性的问题结合二次函数的特点即可获得问题的解答，注意验证．
解答 解：∵△=（3a-2）2-4（a-1）=9a2-16a+8＞0，∴函数f（x）必有两个不相等的零点．
又函数f（x）的图象在区间（-1，3）上与x轴有且只有一个交点，
∴由零点存在性定理，可得f（-1）?f（3）≤0，即（2-2a）?（10a+2）≤0，解得a≤$-\frac{1}{5}$或a≥1．
因此存在实数$a∈（-∞，-\frac{1}{5}]∪[1，+∞）$满足题设条件．
点评 此题考查的是函数与方程的综合应用类问题．在解答的过程当中充分体现了函数与方程的思想、零点存在性知识以及结果验证的技巧．值得同学们体会反思．
练习册系列答案
相关题目
18．直线x=t分别与函数$f（x）=sin（2x-\frac{π}{12}）$、g（x）=$\sqrt{3}cos（2x-\frac{π}{12}）$的图象交于P、Q两点，当实数t变化时，|PQ|的最大值为（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | 1 | D． | $\frac{3}{2}$ |
19．若$sinα=\frac{1}{5}$，则cos2α=（ ）
| A． | $\frac{23}{25}$ | B． | $-\frac{2}{25}$ | C． | $-\frac{23}{25}$ | D． | $\frac{2}{25}$ |
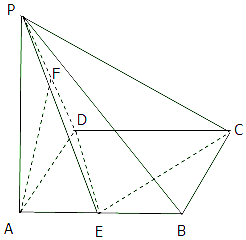已知四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=3，F是PD的中点，E是线段AB上的点．