Question

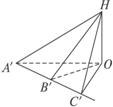
为测量建造中的上海东方明珠电视塔已达到的高度,李明在学校的某一直线上选择A、B、C三点,AB=BC=60 m,且在A、B、C三点观察塔的最高点,测得仰角分别为45°,54.2°,60°,如图,已知李明身高1.5 m,试问建造中的电视塔已达到的高度为多少?(结果保留一位小数)

   

Answer 1

思路分析:设DE=x,则AE、BE、CE都可用x的代数式表示,在△ACE和△BCE中同时用余弦定理列出方程 ,便可求出x.

    解:设塔高DF=h,DE=x,则h=x+1.5.

    在Rt△AED,Rt△BED,Rt△CED中,AE=DE·cot45°=x,BE=DEcot54.2°=xcot54.2°,

CE=DE·cot60°=x.

    在△BEC和△ACE中,由余弦定理得

cos∠BCE==,

    即=.

    解得x≈156.75 m,h=x+1.5=158.3(m).