题目内容
5.已知函数$f(x)=2sin(\frac{1}{3}x-\frac{π}{6})$.用“五点法”画出函数f(x)在一个周期内的图象.分析 根据五点法,求出函数的五点对应的坐标,即可得到结论.
解答 解:列表如下:
| $\frac{1}{3}x-\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |

点评 本题主要考查三角函数图象的做法,利用五点法是解决本题的关键.比较基础.

练习册系列答案
相关题目
16.命题“?x∈R,f(x)<g(x)<h(x)”的否定形式是( )
| A. | ?x0∈R,f(x0)≥g(x0)≥h(x0) | B. | ?x0∈R,f(x0)≥g(x0)或g(x0)≥h(x0) | ||
| C. | ?x∈R,f(x)≥g(x)≥h(x) | D. | ?x∈R,f(x)≥g(x)或g(x)≥h(x) |
17.两条直线l1:2x+y-1=0和l2:x-2y+4=0的交点为( )
| A. | ($\frac{2}{5}$,$\frac{9}{5}$) | B. | (-$\frac{2}{5}$,$\frac{9}{5}$) | C. | ($\frac{2}{5}$,-$\frac{9}{5}$) | D. | (-$\frac{2}{5}$,-$\frac{9}{5}$) |
14.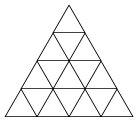 设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
 设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{3}$ |
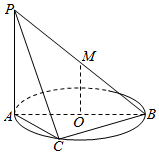 如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题: 已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,$|φ|<\frac{π}{2}$)
已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,$|φ|<\frac{π}{2}$)