题目内容
(2012•泰安一模)等比数列{an}中,已知a1+a2=
,a3+a4=1,则a7+a8的值为
| 1 | 2 |
4
4
.分析:等比数列{an}中,设a5+a6=x,a7+a8=y,由a1+a2=
,a3+a4=1,知
,1,x,y成等比数列,由此能求出a7+a8.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:等比数列{an}中,设a5+a6=x,a7+a8=y,
∵a1+a2=
,a3+a4=1,
∴
,1,x,y成等比数列,
∴x=2,y=4,
∴a7+a8=4.
故答案为:4.
∵a1+a2=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴x=2,y=4,
∴a7+a8=4.
故答案为:4.
点评:本题考查等比数列的通项公式的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
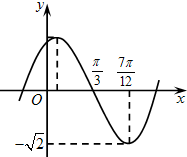 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则