题目内容
（2012•泰安一模）设P={y|y=-x2+1，x∈R}，Q={y|y=2x，x∈R}，则（ ）
分析：根据集合的定义分别求出集合P和Q，再根据子集的定义和补集的定义对A、B、C、D四个选项进行一一验证；
解答：解：∵P={y|y=-x2+1，x∈R}，Q={y|y=2x，x∈R}，
∴P={y|y≤1}，Q={y}y≥0}，
∴P与Q不存在子集的关系，∴A、B错误；
CRP={y|y＞1}，Q={y}y≥0}，
∴CRP⊆Q
故选C．
∴P={y|y≤1}，Q={y}y≥0}，
∴P与Q不存在子集的关系，∴A、B错误；
CRP={y|y＞1}，Q={y}y≥0}，
∴CRP⊆Q
故选C．
点评：本题主要考查集合的包含关系的判断及应用，属于基础题．要正确判断两个集合间的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．
练习册系列答案
相关题目
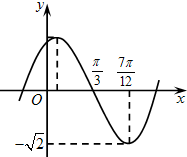（2012•泰安一模）函数f（x）=Asin（ωx+?）（A，ω，?为常数，A＞0，ω＞0）的部分图象如图所示，则