题目内容
（2012•泰安一模）在△ABC中，角A、B、C所对应的边分别为a、b、c，且满足2acosB=bcosC+ccosB．
（I）求角B的大小；
（II）求函数f(A)=2sin2(A+
)-cos(2A+
)的最大值及取得最大值时的A值．
（I）求角B的大小；
（II）求函数f(A)=2sin2(A+
| π |
| 4 |
| π |
| 6 |
分析：（Ⅰ）由2acosB=bcosC+ccosB结合正弦定理可得cosB=
，从而可求角B的大小；
（Ⅱ）由降幂公式与辅助角公式可将f（A）整理为：f（A）=1+
sin（2A-
），由B=
，可求得0＜A＜
，从而可求f（A）的最大值及取得最大值时的A值．
| 1 |
| 2 |
（Ⅱ）由降幂公式与辅助角公式可将f（A）整理为：f（A）=1+
| 3 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
解答：解：（Ⅰ）∵2acosB=bcosC+ccosB，由正弦定理
=
=
=2R得：
2sinAcosB=sinBcosC+cosBsinC…2′
即2sinAcosB=sin（B+C）=sinA，…4′
∴cosB=
，
∴B=
…6′
（Ⅱ）f（A）=2sin2(A+
)-cos（2A+
）
=1-cos（2A+
）-cos（2A+
）
=1+sin2A-
cos2A+
sin2A
=1+
sin2A-
cos2A
=1+
sin（2A-
）…9′
∵在△ABC中，B=
，
∴0＜A＜
，
∴-
＜2A-
＜
，
∴当2A-
=
，即A=
时，f（A）取最大值．
∴f（A）max=1+
…12′
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
2sinAcosB=sinBcosC+cosBsinC…2′
即2sinAcosB=sin（B+C）=sinA，…4′
∴cosB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
（Ⅱ）f（A）=2sin2(A+
| π |
| 4 |
| π |
| 6 |
=1-cos（2A+
| π |
| 2 |
| π |
| 6 |
=1+sin2A-
| ||
| 2 |
| 1 |
| 2 |
=1+
| 3 |
| 2 |
| ||
| 2 |
=1+
| 3 |
| π |
| 6 |
∵在△ABC中，B=
| π |
| 3 |
∴0＜A＜
| 2π |
| 3 |
∴-
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴当2A-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴f（A）max=1+
| 3 |
点评：本题考查三角函数中的恒等变换及正弦定理的应用，突出降幂公式与辅助角公式的应用，属于中档题．
练习册系列答案
相关题目
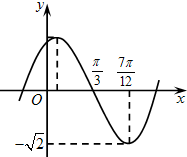（2012•泰安一模）函数f（x）=Asin（ωx+?）（A，ω，?为常数，A＞0，ω＞0）的部分图象如图所示，则