题目内容
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,
, ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
A. 和 和 均为 均为 的最大值. 的最大值. | B. ; ; |
C.公差 ; ; | D. ; ; |
D
解析试题分析:由S5<S6得a1+a2+a3+…+a5<a1+a2+…+a5+a6,即a6>0,
又∵S6=S7,
∴a1+a2+…+a6=a1+a2+…+a6+a7,
∴a7=0,故B正确;
同理由S7>S8,得a8<0,
∵d=a7-a6<0,故C正确;
而D选项S9>S5,即a6+a7+a8+a9>0,可得2(a7+a8)>0,由结论a7=0,a8<0,显然D选项是错误的.
事实上,∵S5<S6,S6=S7>S8,∴S6与S7均为Sn的最大值,故A正确;
故选D.
考点:本题主要考查等差数列的前n项和公式和。
点评:典型题,熟练应用公式是解题的关键。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
设等差数列 的前n项和为
的前n项和为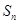 ,若
,若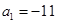 ,
, ,则当
,则当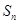 取最小值时,n等于( )
取最小值时,n等于( )
| A.6 | B.7 | C.8 | D.9 |
等差数列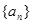 的前
的前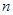 项和为
项和为 ,那么
,那么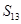 值的是 ( )
值的是 ( )
| A.30 | B.65 | C.70 | D.130 |
已知 为等差数列,若
为等差数列,若 ,则
,则 的值为
的值为
A. | B. | C. | D. |
设数列 的前n项和为
的前n项和为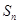 ,令
,令 ,称
,称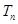 为数列
为数列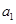 ,
,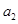 ,……,
,……,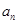 的“理想数”,已知数列
的“理想数”,已知数列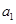 ,
,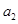 ,……,
,……,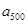 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 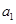 ,
,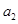 ,……,
,……,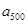 的“理想数”为( )
的“理想数”为( )
| A.2002 | B.2004 | C.2006 | D.2008 |
设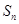 是等差数列{an}的前n项和,
是等差数列{an}的前n项和,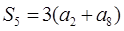 ,则
,则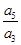 的值为( )
的值为( )
A.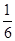 | B.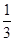 | C.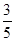 | D.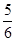 |
已知数列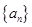 的前n项和
的前n项和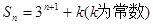 ,那么下述结论正确的是( )
,那么下述结论正确的是( )
A.k为任意实数时,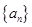 是等比数列 是等比数列 |
B.k =-3时,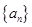 是等比数列 是等比数列 |
C.k =-1时,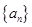 是等比数列 是等比数列 |
D.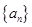 不可能等比数列 不可能等比数列 |
已知等差数列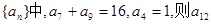 的值是( )
的值是( )
| A.30 | B.15 | C.31 | D.64 |
在等差数列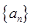 中,
中, 则等差数列
则等差数列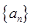 的前13项的和为( )
的前13项的和为( )
| A.104 | B.52 | C.39 | D.24 |