题目内容
在等差数列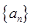 中,
中, 则等差数列
则等差数列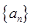 的前13项的和为( )
的前13项的和为( )
| A.104 | B.52 | C.39 | D.24 |
B
解析试题分析:因为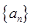 为等差数列,所以
为等差数列,所以 ,
, ,
,
所以 所以
所以 所以等差数列
所以等差数列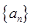 的前13项的和为
的前13项的和为
考点:本小题主要考查等差数列的性质及前n项和公式的应用.
点评:等差数列的性质是解决与等差数列有关的题目的重要依据,要注意灵活应用.

练习册系列答案
相关题目
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,
, ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
A. 和 和 均为 均为 的最大值. 的最大值. | B. ; ; |
C.公差 ; ; | D. ; ; |
在等差数列 中,已知
中,已知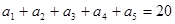 ,那么
,那么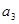 =
=
| A.3 | B.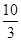 | C.4 | D.5 |
若两个等差数列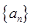 和
和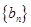 的前
的前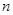 项和分别是
项和分别是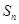 和
和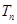 ,已知
,已知 =
=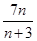 ,则
,则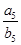 =( )
=( )
| A.7 | B. | C.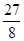 | D. |
等差数列 中,若
中,若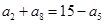 ,则
,则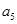 等于
等于
| A.3 | B.4 | C.5 | D.6 |
已知各项均为正数的等比数列{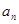 },
},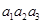 =5,
=5,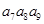 =10,则
=10,则
 =( )
=( )
A.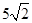 | B.7 | C.6 | D.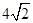 |
已知 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 =
=
| A.8 | B.-8 | C.±8 | D. |
在等差数列 中,3(
中,3( +
+ )+2(a
)+2(a +
+ +
+ )=24,则此数列前13项之和( )
)=24,则此数列前13项之和( )
| A.26 | B.13 | C.52 | D.156 |
由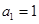 ,
, 确定的等差数列
确定的等差数列 ,当
,当 时,序号
时,序号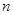 等于( )
等于( )
| A.99 | B.100 | C.96 | D.101 |