题目内容
18.在平面直角坐标系xOy中,已知圆M经过点A(1,0),B(3,0),C(0,1).(1)求圆M的方程;
(2)若直线l“mx-2y-(2m+1)=0与圆M交于点P,Q,且$\overrightarrow{MP}$•$\overrightarrow{MQ}$=0,求实数m的值.
分析 (1)由点的坐标求出弦的中垂线方程,联立求得圆心坐标,再求出半径,则圆的方程可求;
(2)由题意可知∠PMQ=90°,结合圆的半径求出圆心到直线的距离,再由点到直线的距离公式求解.
解答  解:(1)如图,
解:(1)如图,
AB所在直线方程为x=2,AC所在直线方程为y=x,
联立$\left\{\begin{array}{l}{x=2}\\{y=x}\end{array}\right.$,解得M(2,2),
又|MA|=$\sqrt{(2-1)^{2}+(2-0)^{2}}=\sqrt{5}$,
∴圆M的方程为(x-2)2+(y-2)2=5;
(2)∵$\overrightarrow{MP}$•$\overrightarrow{MQ}$=0,∴∠PMQ=90°,
则|PQ|=$\sqrt{10}$,∴M到直线mx-2y-(2m+1)=0的距离为$\frac{\sqrt{10}}{2}$.
由$\frac{|2m-4-2m-1|}{\sqrt{{m}^{2}+4}}=\frac{\sqrt{10}}{2}$,解得:m=$±\sqrt{6}$.
点评 本题考查圆的方程的求法,考查了平面向量的数量积运算,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
6.已知A(1,2),B(3,7),$\overrightarrow{a}$=(x,-1),$\overrightarrow{AB}$∥$\overrightarrow{a}$,则( )
| A. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | B. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相同 | ||
| C. | x=$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 | D. | x=-$\frac{2}{5}$,且$\overrightarrow{AB}$与$\overrightarrow{a}$方向相反 |
10.若直线(a+1)x+2y=0与直线x-ay=1互相垂直,则实数a的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
7.不等式(x-1)(x+2)≤0的解集为( )
| A. | (-2,1) | B. | [-2,1] | C. | (-∞,-2)∪(1,+∞) | D. | (-∞,-2]∪[1,+∞) |
8.已知复数z满足$\frac{z-1}{z+1}=i$,则z等于( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
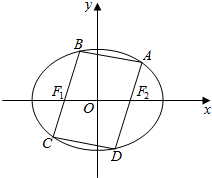 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.