题目内容
1.已知函数f(x)=lnx-px+1(p∈R).(1)当p>$\frac{1}{e}$时,f(x)在区间[1,e]上的最大值为-1,求P的值;
(2)若对任意x1,x2∈(0,+∞),且x1<x2,有f(x1)-x22<f(x2)-x12成立,求p的取值范围.
分析 (1)求出原函数的导函数,由题意可得$\frac{1}{p}$<e,然后分0<$\frac{1}{p}$<1和1≤$\frac{1}{p}$<e求得函数的单调区间,进一步求得f(x)在区间[1,e]上的最大值,由最大值为-1求P的值;
(2)由f(x1)-x22<f(x2)-x12成立,得f(x1)+x12<f(x2)+x22成立,构造函数g(x)=f(x)+x2,由题意可得函数g(x)在(0,+∞)上为增函数,则g′(x)≥0在(0,+∞)上恒成立.转化为△=p2-8≤0或$\left\{\begin{array}{l}{{p}^{2}-8>0}\\{\frac{p}{4}<0}\\{h(0)=1>0}\end{array}\right.$,求解即可得到p的取值范围.
解答 解:(1)∵f(x)=lnx-px+1,x>0,
∴f′(x)=$\frac{1}{x}$-p=$\frac{1-px}{x}$=$\frac{-p(x-\frac{1}{p})}{x}$,
∵p>$\frac{1}{e}$,∴$\frac{1}{p}$<e,
当0<$\frac{1}{p}$<1时,f′(x)<0恒成立,
∴f(x)在[1,e]上单调递减,
∴f(x)max=f(1)=1-p=-1,
解得p=2,满足题意;
当1≤$\frac{1}{p}$<e时,
若f′(x)>0时,即1≤x<$\frac{1}{p}$,函数单调递增,
若f′(x)<0时,即$\frac{1}{p}$<x≤e,函数单调递减,
∴f(x)max=f($\frac{1}{p}$)=ln$\frac{1}{p}$-1+1<-1,舍去.
综上可得:p=2;
(2)由f(x1)-x22<f(x2)-x12成立,得
f(x1)+x12<f(x2)+x22成立,
构造函数g(x)=f(x)+x2,
∵x1,x2∈(0,+∞),且x1<x2,
∴函数g(x)在(0,+∞)上为增函数,则g′(x)≥0在(0,+∞)上恒成立.
∵g(x)=f(x)+x2=lnx-px+1+x2,
∴g′(x)=$\frac{1}{x}-p+2x=\frac{2{x}^{2}-px+1}{x}$(x>0),
则h(x)=2x2-px+1≥0在(0,+∞)上恒成立.
∴△=p2-8≤0或$\left\{\begin{array}{l}{{p}^{2}-8>0}\\{\frac{p}{4}<0}\\{h(0)=1>0}\end{array}\right.$,解得p$≤2\sqrt{2}$.
∴p的取值范围是(-∞,$2\sqrt{2}$].
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,训练了函数构造法,属中档题.

| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
| A. | $\frac{45}{2}$ | B. | 23 | C. | $\frac{47}{2}$ | D. | 24 |
| A. | (-∞,4) | B. | (-$\frac{1}{5}$,2) | C. | (2,4) | D. | (-∞,-$\frac{1}{5}$)∪(2,4) |
 如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n根金属片从1号针移到3号针最小需要移动的次数为f(n),则f(10)1023.
如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n根金属片从1号针移到3号针最小需要移动的次数为f(n),则f(10)1023.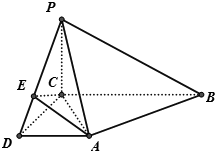 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.