Question

【题目】已知椭圆的左，右焦点为，左，右顶点为，过点的

直线分别交椭圆于点.

（1）设动点，满足，求点的轨迹方程；

（2）当时，求点的坐标；

（3）设，求证：直线过轴上的定点.

Answer 1

【答案】(1)；(2)；(3)证明见解析.

【解析】试题分析：（1）设点P（x，y），由两点距离公式将PF2﹣PB2=4，用点点距写出表示式，整理即得点P的轨迹方程．（2）将分别代入椭圆方程，解出点M与点N的坐标由两点式写出直线AM与直线BN的方程联立解出交点T的坐标．（3）写出两条直线，和椭圆联立得到交点坐标，用MN两点坐标表示直线，从而得到结论。

（1）由题意知:，设，则

， 化简整理得:

（2）把代人椭圆方程,分别求出: ，

直线 ①

直线 ②

由 ①、②得：；

（3）由已知，

直线与椭圆联立，得：

直线与椭圆联立，得：

直线的方程为：

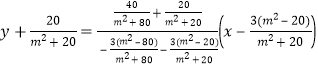
化简得

令，解得，即直线过轴上定点.