题目内容
在坐标系中,分别画出满足不等式的角x的区域,并写出不等式的解集:(1)sinx<-
| 1 |
| 2 |
(2)cosx>
| 1 |
| 2 |
(3)tanx>-1,x∈
(4)cotx>-1,x∈
分析:本题考查的知识点是三角函数的图象及三角函数的单调性,在坐标系中逐一画出正弦函数、余弦函数、正切函数和余切函数的图象,分析后,易给出不等式的解集.
解答:解:(1)正弦函数y=sinx的图象如下图示,由图象可得:当sinx<-
,x∈(-
+2kπ,-
+2kπ)(k∈Z)

(2)余弦函数y=cosx的图象如下图示,由图象可得:当cosx>
,x∈(-
+2kπ,
+2kπ)(k∈Z)

(3)正切函数y=tanx的图象如下图示,由图象可得:当tanx>-1,x∈(-
+2kπ,
+2kπ)(k∈Z)

(4)余切函数y=cotx的图象如下图示,由图象可得:当cotx>-1,x∈(-π+2kπ,-
+2kπ)(k∈Z)
故答案为:(-
+2kπ,-
+2kπ)(k∈Z),(-
+2kπ,
+2kπ)(k∈Z),(-
+2kπ,
+2kπ)(k∈Z),(-π+2kπ,-
+2kπ)(k∈Z)
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 6 |

(2)余弦函数y=cosx的图象如下图示,由图象可得:当cosx>
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |

(3)正切函数y=tanx的图象如下图示,由图象可得:当tanx>-1,x∈(-
| π |
| 4 |
| π |
| 2 |

(4)余切函数y=cotx的图象如下图示,由图象可得:当cotx>-1,x∈(-π+2kπ,-
| π |
| 4 |

故答案为:(-
| 5π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
点评:解三角不等式时,我们常用数形结合的思想进行处理,利用三角函数的图象或单位圆辅助分析.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 已知函数y=f(x)是偶函数,y=g(x)是奇函数,他们的定义域均为[-8,8],下图是在同一坐标系中分别画出的他们的部分 图象,则不等式
已知函数y=f(x)是偶函数,y=g(x)是奇函数,他们的定义域均为[-8,8],下图是在同一坐标系中分别画出的他们的部分 图象,则不等式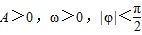 ,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).
,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2). ;
; ;
;