题目内容
已知两函数f(x)=Asin(ωx+φ)和g(x)=Acos(ωx+φ),其中A>0,ω>0,|φ|<
,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).
(1)求A,ω和φ的值;
(2)请在答卷给定的区域中用五点作图法填写列表并在坐标系中画出y=g(x)在长度为一个周期的闭区间上的函数图象.
| π | 2 |
(1)求A,ω和φ的值;
(2)请在答卷给定的区域中用五点作图法填写列表并在坐标系中画出y=g(x)在长度为一个周期的闭区间上的函数图象.
分析:(1)依题意,可求得A,由T=6π可求ω,函数图象过(π,2)可求φ;
(2)依题意得g(x)=2cos(
x+
),列表,作图即可.
(2)依题意得g(x)=2cos(
| 1 |
| 3 |
| π |
| 6 |
解答:(1)由题意知:A=2,…(1分)
∵T=6π,
∴
=6π得
ω=
,…(3分)
∴f(x)=2sin(
x+φ),
∵函数图象过(π,2),
∴sin(
+φ)=1,
∵-
<φ+
<
,
∴φ+
=
,得φ=
…(5分)
∴A=2,ω=
,φ=
ω=
,…(6分)
(2)依题意得g(x)=2cos(
x+
);
作图如下:
 …(10分)…(14分)
…(10分)…(14分)
∵T=6π,
∴
| 2π |
| ω |
ω=
| 1 |
| 3 |
∴f(x)=2sin(
| 1 |
| 3 |
∵函数图象过(π,2),
∴sin(
| π |
| 3 |
∵-
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∴φ+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
∴A=2,ω=
| 1 |
| 3 |
| π |
| 6 |
| 1 |
| 3 |
(2)依题意得g(x)=2cos(
| 1 |
| 3 |
| π |
| 6 |
|
0 |
|
π |
|
2π | ||||||||
| x | -
|
π |
|
4π |
| ||||||||
| g(x) | 2 | 0 | -2 | 0 | 2 |
 …(10分)…(14分)
…(10分)…(14分)点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查五点法作函数y=Asin(ωx+φ)的图象,属于中档题.

练习册系列答案
相关题目
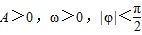 ,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).
,若函数f(x)的图象在y轴右侧的第一个最大值点和第一个最小值点分别为(π,2)和(4π,-2).