题目内容
抛物线y2=2px上不同两点A,B(异于原点O)若OA,OB所在直线斜率之和定值m(m≠0)则直线AB必经过( )
A、(0,
| ||
B、(0,
| ||
C、(-
| ||
D、(-
|
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设出抛物线y2=2px上不同两点A,B的坐标为(
,y1),(
,y2),结合OA,OB所在直线斜率之和定值m,可得
=
,设出直线AB的两点式方程,化简后让x=0,可得直线AB所过定点的坐标.
| ||
| 2p |
| ||
| 2p |
| y1•y2 |
| y1+y2 |
| 2p |
| m |
解答:
解:设点A(
,y1),B(
,y2),
则kOA=
=
,kOB=
=
,
由已知得:
+
=
=m,
即
=
,即
=
,
由直线AB的方程为:
=
,
整理得:y=
,
当x=0时,y=
=
,
故直线必经过(0,
)点,
故选:B
| ||
| 2p |
| ||
| 2p |
则kOA=
| y1 | ||||
|
| 2p |
| y1 |
| y2 | ||||
|
| 2p |
| y2 |
由已知得:
| 2p |
| y1 |
| 2p |
| y2 |
| 2p(y1+y2) |
| y1•y2 |
即
| y1+y2 |
| y1•y2 |
| m |
| 2p |
| y1•y2 |
| y1+y2 |
| 2p |
| m |
由直线AB的方程为:
| y-y2 |
| y1-y2 |
x-
| ||||||||
|
整理得:y=
| 2px+y1•y2 |
| y1+y2 |
当x=0时,y=
| y1•y2 |
| y1+y2 |
| 2p |
| m |
故直线必经过(0,
| 2p |
| m |
故选:B
点评:本题考查的知识点是直线与圆锥曲线的关系,直线的斜率公式,直线的两点式方程,难度中档.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
在复平面内,复数Z=
+i3对应的点位于( )
| 2 |
| 3-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
在△ABC中,下列等式恒成立的是( )
| A、csinA=asinB |
| B、bcosA=acosB |
| C、asinA=bsinB |
| D、asinB=bsinA |
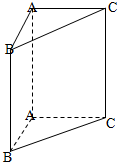 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=