题目内容

一个棱锥的底面是边长为a的正三角形，它的一个侧面也是正三角形，且这个侧面与底面垂直，求这个棱锥的体积和全面积．

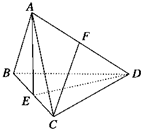解：如图所示，平面ABC⊥平面BCD，△ABC与△BCD均为边长为a的正三角形，
取BC中点E，连接AE，则AE⊥平面BCD，
故棱锥A-BCD的高为AE，△BCD的面积为 $\text{[math]}$ a²，AE= $\text{[math]}$ a，
∴这个棱锥的体积V_A-BCD= $\text{[math]}$ • $\text{[math]}$ a²• $\text{[math]}$ a= $\text{[math]}$ a³．
连接DE，∵AE⊥平面BCD，DE?平面BCD，∴AE⊥DE，
在Rt△AED中，AE=ED= $\text{[math]}$ a，
∴AD= $\text{[math]}$ • $\text{[math]}$ a= $\text{[math]}$ a．
取AD中点F，连接CF，则CF⊥AD．
在Rt△CDF中，DF= $\text{[math]}$ • $\text{[math]}$ a= $\text{[math]}$ a，
∴CF= $\text{[math]}$ a．
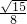∴S_△ACD= $\text{[math]}$ AD•CF= $\text{[math]}$ $\text{[math]}$ a× $\text{[math]}$ a= $\text{[math]}$ a²．
∵△ABD≌△ACD，S_△ABD= $\text{[math]}$ a²．
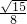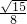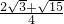故S_全面积= $\text{[math]}$ a²+ $\text{[math]}$ a²+2× $\text{[math]}$ a²= $\text{[math]}$ a²．
分析：棱锥的侧面积等于三个侧面的面积的和，体积利用V= $\text{[math]}$ S_△BCD×AE即可求解．
点评：本题考查棱锥的侧面积和体积，考查空间想象能力，考查学生的计算能力，属于中档题．