题目内容
9．已知集合A={x|x（x-3）＜0}，B={-1，0，1，2，3}，则A∩B=（ ）| A． | {-1} | B． | {1，2} | C． | {0，3} | D． | {-1，1，2，3} |
分析 先分别求出集合A，B，由此利用交集定义能求出A∩B．
解答 解：∵集合A={x|x（x-3）＜0}={x|0＜x＜3}，
B={-1，0，1，2，3}，
∴A∩B={1，2}．
故选：B．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
科学实验活动册系列答案
相关题目
20．定义：如果函数f（x）在[a，b]上存在x1，x2（a＜x1＜x2＜b）满足$f'（{x_1}）=\frac{f（b）-f（a）}{b-a}$，$f'（{x_2}）=\frac{f（b）-f（a）}{b-a}$则称函数f（x）是[a，b]上的“中值函数”．已知函数$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+m$是[0，m]上的“中值函数”，则实数m的取值范围是（ ）
| A． | $（{\frac{3}{4}，1}）$ | B． | $（{\frac{3}{4}，\frac{3}{2}}）$ | C． | $（{1，\frac{3}{2}}）$ | D． | $（{\frac{3}{2}，+∞}）$ |
17．将函数f（x）=2sin（ωx+$\frac{π}{4}$）（ω＞0）的图象向右平移$\frac{π}{4ω}$个单位，得到函数y=g（x）的图象，若y=g（x）在[-$\frac{π}{6}$，$\frac{π}{3}$]上为增函数，则ω的最大值为（ ）
| A． | 3 | B． | 2 | C． | $\frac{3}{2}$ | D． | $\frac{5}{4}$ |
14．在区间（0，4）上任取一实数x，则2x＜2的概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
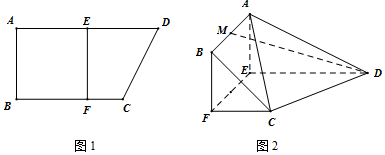
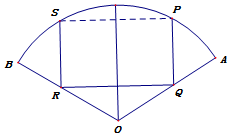如图，扇形OAB的半径为1，圆心角为120°，四边形PQRS是扇形的内接矩形，当其面积最大时，求点P的位置，并求此最大面积．