题目内容
1.某航运公司有6艘可运载30吨货物的A型货船与5艘可运载50吨货物的B型货船,现有每天至少运载900吨货物的任务,已知每艘货船每天往返的次数为A型货船4次和B型货船3次,每艘货船每天往返的成本费为A型货船160元,B型货船252元,那么,每天派出A型货船和B型货船各多少艘,公司所花的成本费最低?分析 设每天派出A型货船和B型货船分别为x艘和y艘,成本为z元,列出约束条件,写出目标函数,画出可行域利用目标函数的几何意义求解即可.
解答 解:设每天派出A型货船和B型货船分别为x艘和y艘,成本为z元,则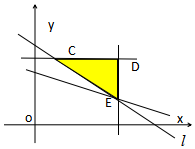
$\left\{\begin{array}{l}0≤x≤6\\ 0≤y≤5\\ 120x+150y≥900\end{array}\right.且x,y∈N$…(4分)
目标函数为z=160x+252y.…(6分)(x,y)满足的可行域如图所示△CDE…(8分)
把z=160x+252y变为$l:y=-\frac{40}{63}x+\frac{1}{252}z$
则得到l是斜率为$-\frac{40}{63}$,在y轴上的截距为$\frac{1}{252}z$,随z变化的一族平行直线.…(9分)
在可行域的整点中,点E(5,2)使得z取得最小值.…(11分)
所以,每天派出A型货船5艘,B型货船2艘,公司所花的成本费最小,最低成本为1304元元. …(12分)
点评 本题考查线性规划的简单应用,列出约束条件以及目标函数,画可行域利用目标函数的几何意义解题的解题的关键,考查数形结合以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知命题p:x2>x是x>1的充分不必要条件;命题q:若数列{an}的前n项和Sn=n2,那么数列{an}是等差数列.则下列命题是真命题的是( )
| A. | p∨(¬q) | B. | p∨q | C. | p∧q | D. | (¬p)∨(¬q) |
6.下列四个命题中真命题为( )
| A. | lg(x2+1)≥0 | B. | 5≤2 | C. | 若x2=4,则x=2 | D. | 若x<2,则$\frac{1}{x}$>$\frac{1}{2}$ |
13.某公司的管理者通过公司近年来科研费用支出x(百万元)与公司所获得利润y(百万元)的散点图发现,y与x之间具有线性相关关系,具体数据如表:
(1)求y对x的回归直线方程;(参考数据:$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=16.3,$\sum_{i=1}^{5}$xiyi=18.5)
(2)若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元,预测2017年该公司可获得的利润为多少万元?
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 科研费用x(百万元) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 公司所获利润y(百万元) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元,预测2017年该公司可获得的利润为多少万元?
11.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于( )
| A. | 20π | B. | 10π | C. | 5π | D. | 5$\sqrt{5}$π |