题目内容
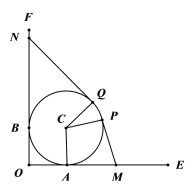
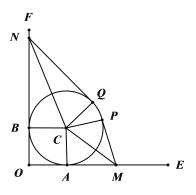
【题目】某地开发一片荒地,如图,荒地的边界是以C为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE,OF,分别与荒地的边界有且仅有一个接触点A,B.现规划修建一条新路(由线段MP,![]() ,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,
,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,![]() 所对的圆心角为
所对的圆心角为![]() .记∠PCA=
.记∠PCA=![]() (道路宽度均忽略不计).
(道路宽度均忽略不计).
(1)若![]() ,求QN的长度;
,求QN的长度;
(2)求新路总长度的最小值.
【答案】(1)QN的长度为1千米(2)![]()
【解析】
(1)连接![]() ,通过切线的几何性质,证得四边形
,通过切线的几何性质,证得四边形![]() 是正方形,由此求得
是正方形,由此求得![]() 的长度.
的长度.
(2)用![]() 表示出线段
表示出线段![]() ,
,![]() ,线段
,线段![]() 的长,由此求得新路总长度的表达式,利用基本不等式求得新路总长度的最小值.
的长,由此求得新路总长度的表达式,利用基本不等式求得新路总长度的最小值.
(1)连接CB,CN,CM,OM⊥ON,OM,ON,PM,QN均与圆C相切
∴CB⊥ON,CA⊥OM,CP⊥MP,CQ⊥NQ,∴CB⊥CA
∵∠PCA=![]()
![]() ,∠PCQ=
,∠PCQ=![]() ,∴∠QCB=
,∴∠QCB=![]() ,
,
此时四边形BCQN是正方形,∴QN=CQ=1,
答:QN的长度为1千米;
(2)∵∠PCA=![]() ,可得∠MCP=
,可得∠MCP=![]() ,∠NCQ=
,∠NCQ=![]() ,
,
则MP=![]() ,
,![]() ,NQ=
,NQ=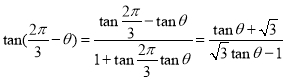
设新路长为![]() ,其中
,其中![]() (
(![]() ,
,![]() ),即
),即![]()
∴![]() ,
,
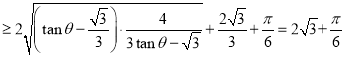 ,当
,当![]() 时取“=”,
时取“=”,
答:新路总长度的最小值为![]() .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目