题目内容
5.已知函数f(x)=$\frac{x}{x+1}$,若数列{an}(n∈N*)满足:a1=1,an+1=f(an)(1)设bn=$\frac{1}{{a}_{n}}$,求证数列{bn}是等差数列;
(2)求数列{an}的通项公式.
分析 (1)根据题意可知,an+1an+an+1=an,即$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,数列{$\frac{1}{{a}_{n}}$}是以1为首项,以1为公差的等差数列,所以数列{bn}是以1为首项,以1为公差的等差数列;
(2)由(1)数列{$\frac{1}{{a}_{n}}$}是以1为首项,以1为公差的等差数列,即可求出答案.
解答 (1)证明:∵f(x)=$\frac{x}{x+1}$,a1=1,an+1=f(an),
∴an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,
∴an+1an+an+1=an,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,
∵a1=1,
∴$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,以1为公差的等差数列,
∵bn=$\frac{1}{{a}_{n}}$,
∴数列{bn}是以1为首项,以1为公差的等差数列;
(2)解:由(1)知,$\frac{1}{{a}_{n}}$=1+(n-1)=n,
∴an=$\frac{1}{n}$.
点评 本题考查等差数列的证明,考查数列的通项公式,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
16.从2015名学生中选50人组成参观团,先用简单随机抽样方法剔除15人,再将其余2000人从0到1999编号,按等距系统抽样方法选取,若第一组采用抽签法抽到的号码是30,则最后一组入选的号码是( )
| A. | 1990 | B. | 1991 | C. | 1989 | D. | 1988 |
20.设方程|x2+3x-3|=a的解的个数为m,则m不可能等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.某市对该市高三年级的教学质量进行了一次检测,某校共有720名学生参加了本次考试,考试结束后,统计了学生在数学考试中,选择选做题A,B,C三题(三道题中必须且只能选一题作答)的答卷份数如表:
该校高三数学备课组为了解参加测试的学生对这三题的答题情况,现用分层抽样的方法从720份答卷中抽出9份进行分析.
(Ⅰ)若从选出的9份答卷中抽出3份,求这3份中至少有1份选择A题作答的概率;
(Ⅱ)若从选出的9份答卷中抽出3份,记其中选择C题作答的份数为X,求X的分布列及其数学期望E(X).
| 题号 | A | B | C |
| 答卷份数 | 160 | 240 | 320 |
(Ⅰ)若从选出的9份答卷中抽出3份,求这3份中至少有1份选择A题作答的概率;
(Ⅱ)若从选出的9份答卷中抽出3份,记其中选择C题作答的份数为X,求X的分布列及其数学期望E(X).
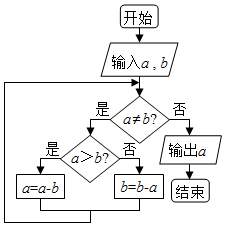 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若在框图中输入的a,b分别为30、18,则输出的a为( )