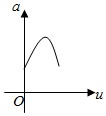题目内容
16.在△ABC中,三个内角分别是A、B、C,向量$\overrightarrow{a}$=($\frac{\sqrt{5}}{2}$cos$\frac{C}{2}$,cos$\frac{A-B}{2}$),当tanA•tanB=$\frac{1}{9}$时,则|$\overrightarrow{a}$|=$\frac{3\sqrt{2}}{4}$.分析 根据向量模的定义和三角函数的化简即可求出答案.
解答 解:∵向量$\overrightarrow{a}$=($\frac{\sqrt{5}}{2}$cos$\frac{C}{2}$,cos$\frac{A-B}{2}$),
∴|$\overrightarrow{a}$|2=($\frac{\sqrt{5}}{2}$cos$\frac{C}{2}$,cos$\frac{A-B}{2}$)=$\frac{5}{4}$cos2$\frac{C}{2}$+cos2$\frac{A-B}{2}$
=$\frac{5}{8}$(cosC+1)+$\frac{1}{2}$[cos(A-B)+1]=-$\frac{5}{8}$cos(A+B)+$\frac{1}{2}$cos(A+B)+$\frac{9}{8}$
=-$\frac{5}{8}$(cosAcosB-sinAsinB)+$\frac{1}{2}$(cosAcosB+sinAsinB)+$\frac{9}{8}$=-$\frac{1}{8}$cosAcosB+$\frac{9}{8}$sinAsinB+$\frac{9}{8}$,
∵tanA•tanB=$\frac{1}{9}$,
∴sinAsinB=$\frac{1}{9}$cosAcosB,
∴|$\overrightarrow{a}$|2=$\frac{9}{8}$,
∴|$\overrightarrow{a}$|=$\frac{3\sqrt{2}}{4}$,
故答案为:$\frac{3\sqrt{2}}{4}$
点评 本题考查了向量的模和三角形函数的化简和求值,关键是掌握二倍角公式,属于中档题

练习册系列答案
相关题目
11.下列函数是偶函数的是( )
| A. | y=x | B. | y=3x2 | C. | y=x-1 | D. | y=|x|(x∈[0,1]) |
1.已知全集U={1,2,3,4,5},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A. | {4} | B. | {2,4,5} | C. | {1,2,3,4} | D. | {1,2,4,5} |
8.三棱锥P-ABC的两侧面PAB、PBC都是边长为2的正三角形,AC=$\sqrt{3}$,则二面角A-PB-C的大小为( )

| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
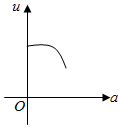
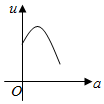
 如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )