题目内容
6.已知等差数列{an}中,a1=1,a2>1,a2,a4,a9成等比数列.(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn.
分析 (1)设等差数列{an}的公差为d,由题意可得d>0,再由等比数列中项性质,解方程可得公差d,即可得到所求通项公式;
(2)运用等差数列的求和公式,计算化简即可得到.
解答 解:(1)设等差数列{an}的公差为d,∵a1=1,a2>1,
∴d=a2-a1>0.
∵a2、a4、a9成等比数列,
∴$a_4^2={a_2}{a_9}$,即(1+3d)2=(1+d)(1+8d).
解得,d=3.
an=a1+(n-1)d=1+3(n-1)=3n-2;
(2)由(1)知,Sn=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{n(1+3n-2)}{2}$=$\frac{3}{2}$n2-$\frac{1}{2}$n.
点评 本题考查等差数列的通项公式和求和公式,以及等比数列的中项性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
14.将函数$y=sin(x+\frac{π}{3})$的图象向x轴正方向平移$\frac{π}{6}$个单位后,得到的图象解析式是( )
| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(x-\frac{π}{6})$ | C. | $y=sin(x-\frac{2π}{3})$ | D. | $y=sin(x+\frac{2π}{3})$ |
1.已知双曲线$\frac{{x}^{2}}{(m+1)^{2}}$-$\frac{{y}^{2}}{{m}^{2}}$=1(m>0)的离心率为$\frac{{\sqrt{5}}}{2}$,P是该双曲线上的点,P在该双曲线两渐近线上的射影分别是A,B,则|PA|•|PB|的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
11.如图某几何体的三视图是直角边长为1的三个等腰直角三角形,则该几何体的外接球的表面积为( )
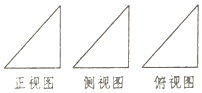

| A. | $\frac{3}{2}π$ | B. | $\sqrt{3}π$ | C. | $\frac{{\sqrt{3}}}{2}π$ | D. | 3π |
16.某赛季甲、乙两名篮球运动员每场比赛得分如图所示,则甲、乙两运动员得分的中位数分别是( )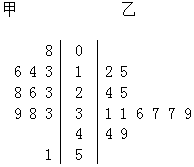

| A. | 26 33.5 | B. | 26 36 | C. | 23 31 | D. | 24.5 33.5 |