题目内容

已知点E在△ABC所在的平面且满足
AB
+
AC
=λ
AE
(λ≠0)，则点E一定落在（　　）
分析：根据平行四边形法则，可得E一定落在这个平行四边形的起点为A的对角线上，利用平行四边形对角线互相平分，即可得到结论．
解答：解：因为点E在△ABC所在的平面且满足
AB
+
AC
=λ
AE
(λ≠0)
所以，根据平行四边形法则，E一定落在这个平行四边形的起点为A的对角线上，
又平行四边形对角线互相平分，所以E一定落在BC边的中线所在的直线上，
故选B．
点评：本题考查向量在几何中的应用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
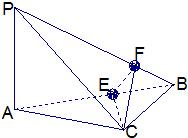精英家教网如图所示，在四面体P-ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=2
34
．F是线段PB上一点，CF=
15
17
34
，点E在线段AB上，且EF⊥PB．
（1）证明：PB⊥平面CEF；
（2）求二面角B-CE-F的大小．
如图，在三棱锥P-ABC中，PA=PB=
2
，AC=BC=1，∠ACB=∠PAC=∠PBC=90°，D为AB的中点．
（Ⅰ）求证：平面PDC⊥平面ABC；
（Ⅱ）求点P到平面ABC的距离；
（Ⅲ）已知点E在线段PB上，且BE=1，求EC与平面ABC所成的角．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（不等式选做题）不等式|
x+1
x-1
|≥1的解集是
（-∞，0]
（-∞，0]
．
B．（几何证明选做题） 如图，以AB=4为直径的圆与△ABC的两边分别交于E，F两点，∠ACB=60°，则EF=
2
2
．
C．（坐标系与参数方程选做题） 在极坐标中，已知点P为方程ρ（cosθ+sinθ）=1所表示的曲线上一动点，Q（2，
π
3
），则|PQ|的最小值为
6
2
6
2
．

如图所示，已知点D在△ABC内，点E在△ABC外，且∠BAD＝∠BCE，∠ABD＝∠CBE．求证：AC·BE＝BC·DE．
如图，在三棱锥P-ABC中，，∠ACB=∠PAC=∠PBC=90°，D为AB的中点．
（Ⅰ）求证：平面PDC⊥平面ABC；
（Ⅱ）求点P到平面ABC的距离；
（Ⅲ）已知点E在线段PB上，且BE=1，求EC与平面ABC所成的角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网