题目内容
19．
如图所示的是一个三棱台ABC-A1B1C1，如何用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．
分析 根据棱台的几何特征和棱锥的几何特征，先将棱台分成一个三棱锥和四棱锥，再把四棱锥沿对角面切开，可得答案．
解答 解：如下图所示：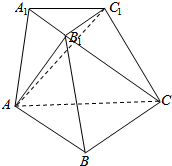
平面AB1C1和平面AB1C能把三棱台分成三部分，且每一部分都是一个三棱锥．
点评 本题考查的知识点是棱台的几何特征，棱锥的几何特征，难度不大，属于基础题．
练习册系列答案
相关题目
9．已知有穷数列5，7，9，…，2n+7（n为偶数），则9+n是该数列的（ ）
| A． | 第n+1项 | B． | 第n+2项 | C． | 第$\frac{n}{2}$+2项 | D． | 第$\frac{n}{2}$+3项 |
10．
将甲、乙两名学生近5次生物考试成绩，制成如图所示的茎叶图，考虑以下结论：
①甲生的平均成绩大于乙生的平均成绩；
②甲生的平均成绩小于乙生的平均成绩；
③甲生成绩的方差大于乙生成绩的方差；
④甲生成绩的方差小于乙生成绩的方差．
其中根据茎叶图能得到正确的统计结论的编号为（ ）
将甲、乙两名学生近5次生物考试成绩，制成如图所示的茎叶图，考虑以下结论：①甲生的平均成绩大于乙生的平均成绩；
②甲生的平均成绩小于乙生的平均成绩；
③甲生成绩的方差大于乙生成绩的方差；
④甲生成绩的方差小于乙生成绩的方差．
其中根据茎叶图能得到正确的统计结论的编号为（ ）
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
14．数列{an}的通项公式an=-58+16n-n2，则（ ）
| A． | {an}是递增数列 | B． | {an}是递减数列 | ||
| C． | {an}先增后减，有最大值 | D． | {an}先减后增，有最小值 |
如图所示，圆锥底面的圆的半径OA=6，轴截面的顶角∠ASB是直角，过两条母线的截面SCB截去底面圆周的$\frac{1}{6}$，求截面的面积．
19．
函数f（x）=Asin（ωx+φ）的部分图象如图所示，则函数f（x）的周期为（ ）
函数f（x）=Asin（ωx+φ）的部分图象如图所示，则函数f（x）的周期为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{3}{4}π$ | C． | π | D． | 2π |