题目内容
设等差数列{an}与{bn}的前n项之和分别为Sn与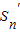 ,若
,若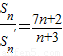 ,则
,则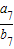 = .
= .
【答案】分析:利用等差数列的性质S2n-1=(2n-1)•an,S′2n-1=(2n-1)•bn即可求得 .
.
解答:解:∵{an}为等差数列,其前n项之和为Sn,
∴S2n-1=
=
=(2n-1)•an,
同理可得,S′2n-1=(2n-1)•bn,
∴ =
= ,
,
又 =
= ,
,
∴ =
= =
= ,
,
∴ =
= ,
,
∴ =
= .
.
故答案为: .
.
点评:本题考查等差数列的性质,求得 =
= 是关键,考查熟练应用等差数列解决问题的能力,属于中档题.
是关键,考查熟练应用等差数列解决问题的能力,属于中档题.
 .
.解答:解:∵{an}为等差数列,其前n项之和为Sn,
∴S2n-1=

=

=(2n-1)•an,
同理可得,S′2n-1=(2n-1)•bn,
∴
 =
= ,
,又
 =
= ,
,∴
 =
= =
= ,
,∴
 =
= ,
,∴
 =
= .
.故答案为:
 .
.点评:本题考查等差数列的性质,求得
 =
= 是关键,考查熟练应用等差数列解决问题的能力,属于中档题.
是关键,考查熟练应用等差数列解决问题的能力,属于中档题. 
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
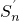 ,若
,若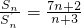 ,则
,则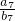 =________.
=________.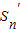 ,若
,若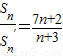 ,则
,则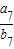 = .
= .