题目内容
若方程x2-3x-1=0的两根分别是x1和x2,求
+
的值.
| 1 |
| x1 |
| 1 |
| x2 |
考点:函数的零点与方程根的关系
专题:计算题,函数的性质及应用
分析:由二次方程根与系数的关系可得x1+x2=3,x1x2=-1,从而求解.
解答:
解:∵方程x2-3x-1=0的两根分别是x1和x2,
∴x1+x2=3,x1x2=-1;
故
+
=
=
=-3.
∴x1+x2=3,x1x2=-1;
故
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 3 |
| -1 |
点评:本题考查了根与系数的关系应用,属于中档题.

练习册系列答案
相关题目
绝对值等于其相反数的数一定是( )
| A、负数 | B、正数 |
| C、负数或零 | D、正数或零 |
抛物线y=(x-2)2+3的对称轴是( )
| A、直线x=-3 |
| B、直线x=3 |
| C、直线x=-2 |
| D、直线x=2 |
已知单位向量
,
夹角为
,则|2
-
|=( )
| a |
| b |
| π |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
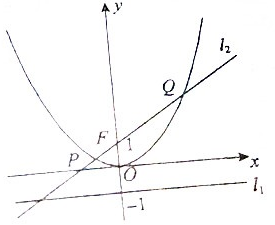 已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.
已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E. 已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.
已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.