Question

（2009•普陀区二模）如图，圆锥体是由直角三角形AOC绕直角边AO所在直线旋转一周所得，OC=2．设点B为圆锥体底面圆周上一点，∠BOC=60°，且△ABC的面积为3．求该圆锥体的体积．

Answer 1

分析：设出BC中点为D，做出辅助线连接AD，OD根据OB=OC=2，∠BOC=60°，得到△OBC为等边三角形，表示出三角形的面积，得到AD的长度，进而得到圆锥的高，求出圆锥的体积．

解答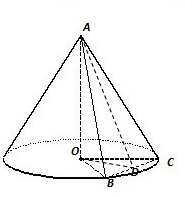：解：如图，设BC中点为D，连接AD，OD
由题意，OB=OC=2，∠BOC=60°，所以△OBC为等边三角形
故BC=2，且OD=

3

又S_△ABC=

1

2

BC×AD=3，得AD=3
所以AO=

AD2-OD2

=

6

而圆锥体的底面圆面积为S=π×OC²=4π
所以圆锥体的体积是V=

1

3

×S_△ABC×AO=

4 6 π

3

点评：本题考查旋转体，本题要求圆锥的体积，解题的关键是求出圆锥的高，这里有应用三角形的性质来求解高的过程，本题是一个中档题目．