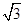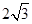题目内容
已知平面向量
与
不共线,若存在非零实数x,y,使得
=
+2x
,
=-y
+2(2-x2)
.
(1)当
=
时,求x,y的值;
(2)若
=(cos
,sin(-
)),
=(sin
,cos
),且
⊥
,试求函数y=f(x)的表达式.
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
(1)当
| c |
| d |
(2)若
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| π |
| 6 |
| π |
| 6 |
| c |
| d |
(1)由条件得:
+2x
=-y
+(4-2x2)
,
∴(1+y)
+(2x-4+2x2)
=
,
∵向量
与
不共线,
∴
,解得y=-1,x=1或x=-2.
(2)∵
•
=cos
sin
+sin(-
)cos
=0,∴
⊥
又∵
⊥
,∴
•
=0,又由条件可知,|
|=|
|=1
∴
•
=(
+2x
)•[-y
+(4-2x2)
]
=-y
2-2xy
•
+(4-2x2)
•
+2x(4-2x2)
2
=-y+2x(4-2x2)=0,∴y=8x-4x3,
即f(x)=8x-4x3
| a |
| b |
| a |
| b |
∴(1+y)
| a |
| b |
| 0 |
∵向量
| a |
| b |
∴
|
(2)∵
| a |
| b |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| a |
| b |
又∵
| c |
| d |
| c |
| d |
| a |
| b |
∴
| c |
| d |
| a |
| b |
| a |
| b |
=-y
| a |
| a |
| b |
| a |
| b |
| b |
=-y+2x(4-2x2)=0,∴y=8x-4x3,
即f(x)=8x-4x3

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
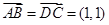 ,
,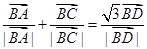 ,则四边形ABCD的面积为( )
,则四边形ABCD的面积为( )