题目内容
(本小题满分14分) 设函数 ,
, .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)若存在 ,使得
,使得 成立,求满足条件的最大整数
成立,求满足条件的最大整数 ;
;
(Ⅲ)如果对任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(Ⅰ) ①当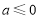 时,函数
时,函数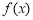 在
在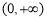 上单调递增,②当
上单调递增,②当 时,函数
时,函数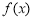 的单调递增区间为
的单调递增区间为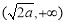 ,函数
,函数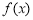 的单调递减区间为
的单调递减区间为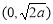 ;
;
(Ⅱ)18;(Ⅲ)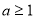 。
。
【解析】
试题分析:(Ⅰ)对函数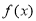 求导,根据
求导,根据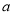 的不同取值,讨论
的不同取值,讨论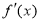 的符号,即可函数
的符号,即可函数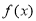 的单调性;
的单调性;
(Ⅱ) 存在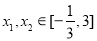 ,使得
,使得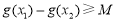 等价于在区间
等价于在区间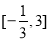 上,
上,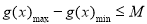 ,对函数
,对函数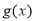 求导,研究其单调性与最值即可;
求导,研究其单调性与最值即可;
(Ⅲ)任意的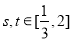 ,都有
,都有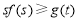 成立等价于在区间
成立等价于在区间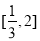 上,函数
上,函数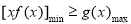 ,由导数与函数单调性与最值关系,分别求函数
,由导数与函数单调性与最值关系,分别求函数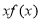 的最小值与函数
的最小值与函数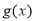 的最大值,解不等式即可.
的最大值,解不等式即可.
试题解析:(Ⅰ)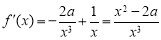 , 定义域(0,
, 定义域(0, ) 1分
) 1分
①当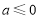 时,
时,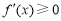 ,函数
,函数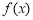 在
在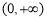 上单调递增, 2分
上单调递增, 2分
②当 时,
时,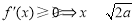 ,函数
,函数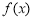 的单调递增区间为
的单调递增区间为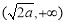 .
.
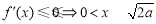 ,函数
,函数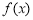 的单调递减区间为
的单调递减区间为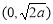 . 4分
. 4分
(Ⅱ)存在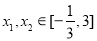 ,使得
,使得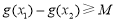 成立,
成立,
等价于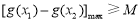 . 5分
. 5分
考察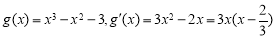
|
|
| 0 |
|
|
| 3 |
| + | 0 | - | 0 | + | ||
|
| 递增 |
| 递减 |
| 递增 | 15 |
由上表可知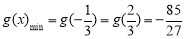 ,
,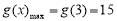
 ,
,
所以满足条件的最大整数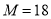 . 9分
. 9分
(Ⅲ)当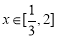 时,由(Ⅱ)可知,
时,由(Ⅱ)可知,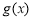 在
在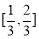 上是减函数,
上是减函数,
在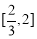 上增函数,而
上增函数,而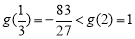
 的最大值是1. 10分
的最大值是1. 10分
要满足条件,则只需当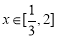 时,
时, 恒成立,
恒成立,
等价于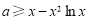 恒成立,
恒成立,
记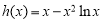 ,
,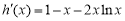 ,
,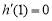 . 11分
. 11分
当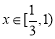 时,
时,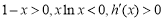 即函数
即函数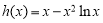 在区间
在区间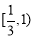 上递增,
上递增,
当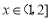 时,
时,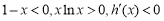 即函数
即函数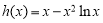 在区间
在区间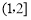 上递减,
上递减,
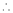
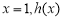 取到极大值也是最大值
取到极大值也是最大值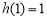 . 13分
. 13分
所以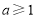 . 14分
. 14分
另解:设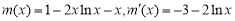 ,
,
由于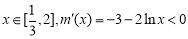 ,
,
所以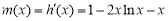 在
在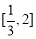 上递减,又
上递减,又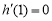
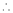 当
当 时,
时,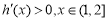 时
时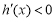 ,
,
即函数 在区间
在区间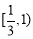 上递增,在区间
上递增,在区间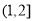 上递减, 13分
上递减, 13分
所以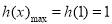 ,所以
,所以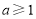 . 14分
. 14分
考点:导数与函数单调性、极值、最值,不等式恒成立问题的化归与转化.

 阅读快车系列答案
阅读快车系列答案









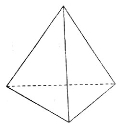
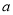 的正方形的四棱锥
的正方形的四棱锥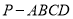 中,已知
中,已知 ,且
,且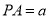 ,则直线
,则直线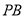 与平面
与平面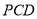 所成的角的余弦值为( )
所成的角的余弦值为( )
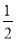 B.
B.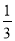 C.
C. D.
D.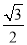
 ∶
∶ ∶
∶
 ∶
∶ ∶
∶ ,则角
,则角 .
. 若
若 ,则函数
,则函数 在区间
在区间 内
内  ,设函数
,设函数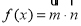 .
. 在区间
在区间 上的零点;
上的零点;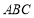 中,角
中,角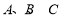 的对边分别是
的对边分别是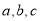 ,且满足
,且满足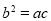 ,求
,求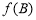 的取值范围.
的取值范围.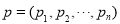 ,
, 的蔡查罗和(蔡查罗是一位数学家)定义为
的蔡查罗和(蔡查罗是一位数学家)定义为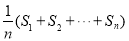 ,其中
,其中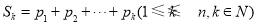 .若一个99项的数列(
.若一个99项的数列(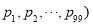 的蔡查罗和为1000,那么100项数列
的蔡查罗和为1000,那么100项数列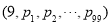 的蔡查罗和为
的蔡查罗和为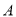 ,
,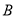 间的距离,某同学首先选定了与
间的距离,某同学首先选定了与 ,然后给出了四种测量方案:(△
,然后给出了四种测量方案:(△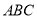 的角
的角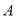 ,
,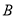 ,
,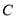 所对的边分别记为
所对的边分别记为 ,
,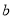 ,
,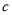 )
)
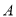 ,
,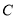 ,
,
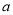 ,
,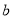 ,
,
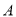 ,
,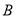 ,
,