题目内容
(本题满分16分)已知函数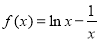 ,
, .
.
(1)若函数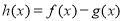 在
在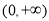 上单调递增,求实数
上单调递增,求实数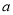 的取值范围;
的取值范围;
(2)若直线 是函数
是函数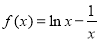 图象的切线,求
图象的切线,求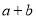 的最小值;
的最小值;
(3)当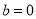 时,若
时,若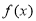 与
与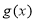 的图象有两个交点
的图象有两个交点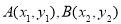 ,求证:
,求证: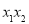
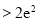 .(取
.(取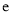 为
为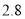 ,取
,取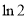 为
为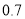 ,取
,取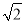 为
为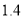 )
)
(1)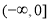 (2)
(2)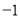 .(3)详见解析
.(3)详见解析
【解析】
试题分析:(1)由题意得对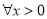 ,
,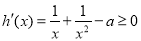 恒成立,即
恒成立,即 ,∵
,∵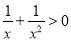 ,∴
,∴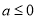 (2)设切点
(2)设切点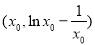 ,由导数几何意义得
,由导数几何意义得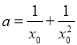 ,
,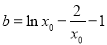 ,令
,令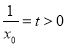 ,则
,则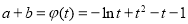 ,问题就转化为利用导数求最值:由
,问题就转化为利用导数求最值:由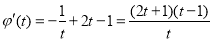 得当
得当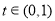 时 ,
时 ,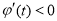 ,
,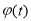 在
在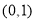 上单调递减;当
上单调递减;当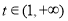 时,
时,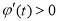 ,
,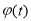 在
在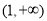 上单调递增,∴
上单调递增,∴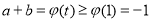 ,故
,故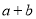 的最小值为
的最小值为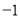 .(3)本题较难,难点在于构造函数.先根据等量关系消去参数a:由题意知
.(3)本题较难,难点在于构造函数.先根据等量关系消去参数a:由题意知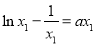 ,
,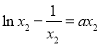 ,两式相加得
,两式相加得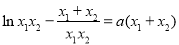 ,两式相减得
,两式相减得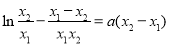 ,即
,即 ,
,
∴ ,即
,即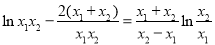 ,为研究等式右边范围构造函数
,为研究等式右边范围构造函数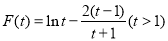 ,易得
,易得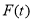 在
在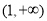 上单调递增,因此当
上单调递增,因此当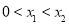 时,有
时,有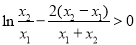 即
即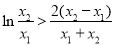 ,所以
,所以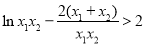 ,再利用基本不等式进行放缩:
,再利用基本不等式进行放缩: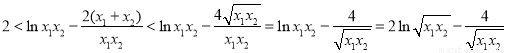 ,
,
即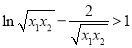 ,再一次构造函数
,再一次构造函数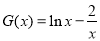 ,易得其在
,易得其在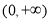 上单调递增,而
上单调递增,而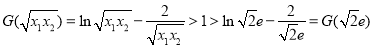 ,因此
,因此 ,即
,即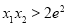 .
.
试题解析:【解析】
(1)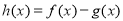
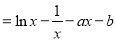 ,则
,则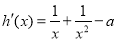 ,
,
∵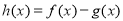 在
在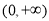 上单调递增,∴对
上单调递增,∴对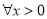 ,都有
,都有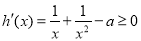 ,
,
即对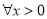 ,都有
,都有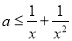 ,∵
,∵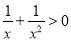 ,∴
,∴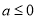 ,
,
故实数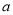 的取值范围是
的取值范围是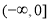 . 4分
. 4分
(2)设切点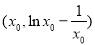 ,则切线方程为
,则切线方程为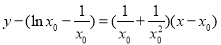 ,
,
即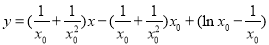 ,亦即
,亦即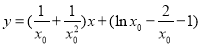 ,
,
令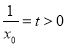 ,由题意得
,由题意得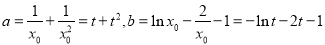 , 7分
, 7分
令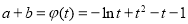 ,则
,则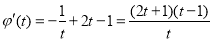 ,
,
当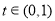 时 ,
时 ,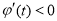 ,
,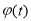 在
在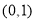 上单调递减;
上单调递减;
当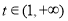 时,
时,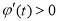 ,
,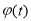 在
在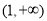 上单调递增,
上单调递增,
∴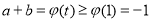 ,故
,故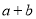 的最小值为
的最小值为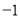 . 10分
. 10分
(3)由题意知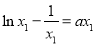 ,
,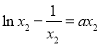 ,
,
两式相加得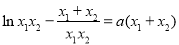 ,两式相减得
,两式相减得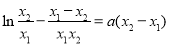 ,
,
即 ,∴
,∴ ,
,
即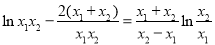 , 12分
, 12分
不妨令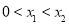 ,记
,记 ,令
,令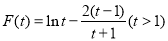 ,则
,则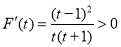 ,
,
∴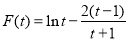 在
在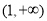 上单调递增,则
上单调递增,则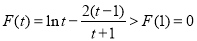 ,
,
∴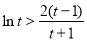 ,则
,则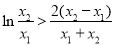 ,∴
,∴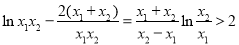 ,
,
又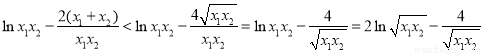 ,
,
∴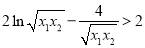 ,即
,即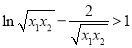 ,
,
令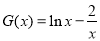 ,则
,则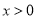 时,
时,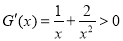 ,∴
,∴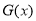 在
在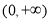 上单调递增,
上单调递增,
又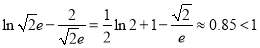 ,
,
∴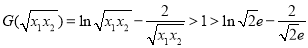 ,则
,则 ,即
,即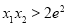 .
.
16分
考点:导数几何意义,导数综合应用
考点分析: 考点1:导数在研究函数中的应用 考点2:函数的单调性与导数 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +loga
+loga (a>0且a≠1),且f(m)=7(m≠0),则f(﹣m)=.
(a>0且a≠1),且f(m)=7(m≠0),则f(﹣m)=. 如下:
如下: ,且当
,且当 时,
时, ,其中
,其中 是不同的质数.
是不同的质数. 为12的全部不同正因数的集合,则
为12的全部不同正因数的集合,则 .
.


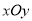 中,角
中,角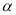 的终边经过点
的终边经过点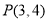 .
.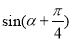 的值;
的值;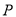 关于
关于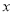 轴的对称点为
轴的对称点为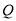 ,求
,求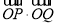 的值.
的值. 中,
中, ,
, ,则数列的前
,则数列的前 项和为 .
项和为 .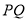 为斜边的等腰直角三角形
为斜边的等腰直角三角形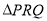 构成,其中
构成,其中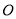 为
为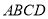 ,按实际需要,四边形
,按实际需要,四边形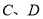 分别在线段
分别在线段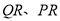 上,另外两个顶点
上,另外两个顶点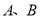 在半圆上,
在半圆上, 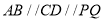 ,且
,且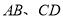 间的距离为1km.设四边形
间的距离为1km.设四边形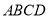 的周长为
的周长为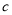 km.
km.
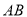 长;
长;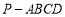 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,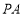 ⊥
⊥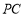 ,
,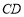 ⊥
⊥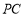 ,
, ,
,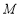 分别是
分别是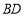 ,
,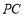 的中点,连结
的中点,连结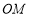 .求证:
.求证: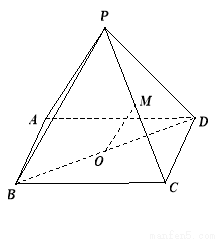
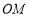 ∥平面
∥平面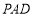 ;
;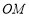 ⊥平面
⊥平面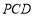 .
.