题目内容
在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC与不同的两点M,N,若
=m
,
=n
,m>0,n>0,则
+
的最小值为( )
| AB |
| AM |
| AC |
| AN |
| 1 |
| m |
| 4 |
| n |
分析:三点共线时,以任意点为起点这三点为终点的三向量,其中一向量可用另外两向量线性表示且其系数和为1.
+
=1的妙用会使问题简单化.
| m |
| 2 |
| n |
| 2 |
解答:解:∵点O是BC的中点,∴
=
(
+
)
又
=m
,
=n
,m>0,n>0∴
=
+
∵M、O、N三点共线,∴
+
=1
故
+
=(
+
)(
+
)=
+
+
≥
+2
=
当且仅当
=
,即m=
,n=
时取到等号,故
+
的最小值为:
故选C.
| AO |
| 1 |
| 2 |
| AB |
| AC |
又
| AB |
| AM |
| AC |
| AN |
| AO |
| m |
| 2 |
| AM |
| n |
| 2 |
| AN |
∵M、O、N三点共线,∴
| m |
| 2 |
| n |
| 2 |
故
| 1 |
| m |
| 4 |
| n |
| 1 |
| m |
| 4 |
| n |
| m |
| 2 |
| n |
| 2 |
| 5 |
| 2 |
| n |
| 2m |
| 2m |
| n |
| 5 |
| 2 |
|
| 9 |
| 2 |
当且仅当
| n |
| 2m |
| 2m |
| n |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| m |
| 4 |
| n |
| 9 |
| 2 |
故选C.
点评:本题主要考查了基本不等式在求解函数的最值中的应用,解题的关键是根据已知向量的知识寻求基本不等式的条件,属基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
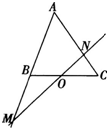 如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB、AC于不同的两点M、N,若
如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB、AC于不同的两点M、N,若 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若