题目内容

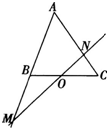精英家教网如图，在△ABC中，点O是BC的中点．过点O的直线分别交直线AB、AC于不同的两点M、N，若
AB
=m
AM
，
AC
=n
AN
，则m+n的值为
 
．
分析：三点共线时，以任意点为起点，这三点为终点的三向量，其中一向量可用另外两向量线性表示，其系数和为一．
解答：解：
AO
=
1
2
（
AB
+
AC
）
=
m
2
AM
+
n
2
AN
，
∵M、O、N三点共线，
∴
m
2
+
n
2
=1，
∴m+n=2．
故答案：2
点评：本题考查三点共线的充要条件．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
AD=4cm．
（1）求：⊙O的直径BE的长；
（2）计算：△ABC的面积．
精英家教网如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
3
BD，BC=2BD，则sinC的值为（　　）
A、
3
3
B、
3
6
C、
6
3
D、
6
6
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
（1）求∠ADC的大小；
（2）求AB的长．
如图，在△ABC中，已知
BD
=2
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网