题目内容
已知函数 =
= 。
。
(1)当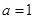 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)求函数 在区间
在区间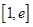 上的最小值;
上的最小值;
(3)在(1)的条件下,设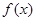 =
= +
+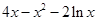 ,
,
求证: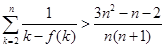 (
(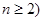 ),参考数据:
),参考数据: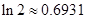 。(13分)
。(13分)
(1)单调增区间是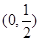 ,
,
 ;
;
(2)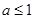 时,
时,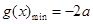 ;
; 时,
时,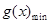 =
=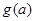 =
=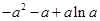 ;
;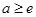 时,
时,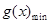 =
=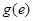 =
=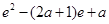 .
.
(3)证明详见解析.
解析试题分析:(1)求f(x)的导函数f′(x),讨论a的值使f′(x)>0时对应f(x)单调增,
f′(x)<0时,对应f(x)单调减;
(2)结合(1),讨论a的取值对应f(x)在区间[1,e]内的单调性,从而求得f(x)在区间[1,e]内的最小值.
试题解析:(1)当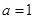 时,
时, =
= ,
, ,得
,得 或
或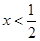 ,故
,故 的单调增区间是
的单调增区间是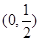 ,
,
 。 3分
。 3分
(2) =
= ,
,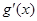 =
= =
= ,
,
令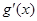 =0得
=0得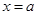 或
或
 。
。
当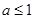 时,
时,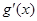
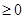 ,
, 递增,
递增,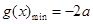 ; 6分
; 6分
当 时,
时, ,
,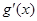 <0,
<0, 递减;
递减;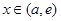 ,
,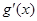
 ,
, 递增,
递增,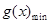 =
=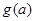 =
=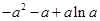 7分
7分
当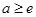 时,
时,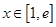 ,
,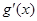
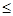 0,
0, 递减,
递减,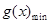 =
=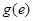 =
=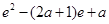 …8分
…8分
(3)令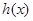 =
=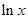 —
—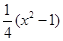 ,
,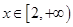 。
。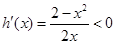 ,
,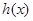 递减,
递减,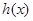
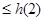 ,
, ,∴
,∴ 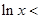
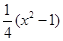 ,
,
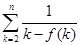 =
= =
=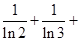 …
…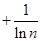
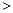
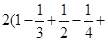 …
… =
= (
(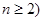 )……13分
)……13分
考点:1.利用导数研究函数的单调性;2.利用导数求闭区间上函数的最值.3.利用导数的性质证明不等式.

练习册系列答案
相关题目
 .
. 在x=
在x= 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值; 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为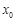 ,证明
,证明 .
. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.
平行. 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根?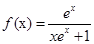 .
.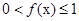 ;
;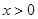 时,
时,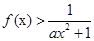 ,求
,求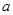 的取值范围.
的取值范围. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调性.
的单调性.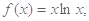
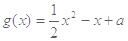 .
.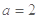 时,求
时,求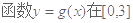 上的值域;
上的值域;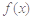 在
在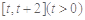 上的最小值;
上的最小值;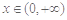 ,都有
,都有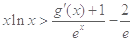 成立
成立 ,其中
,其中 为常数.
为常数. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; ,求函数
,求函数 上是增函数的概率.
上是增函数的概率.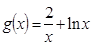 ,
,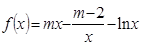 ,
,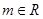 .
.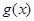 的极值点;
的极值点;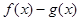 在
在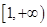 上为单调函数,求
上为单调函数,求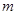 的取值范围;
的取值范围;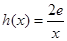 ,若在
,若在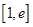 上至少存在一个
上至少存在一个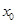 ,使得
,使得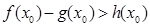 成立,求
成立,求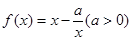 ,
,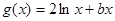 ,且直线
,且直线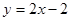 与曲线
与曲线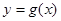 相切.
相切.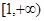 内的一切实数
内的一切实数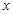 ,不等式
,不等式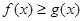 恒成立,求实数
恒成立,求实数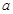 的取值范围;
的取值范围;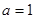 时,求最大的正整数
时,求最大的正整数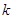 ,使得任意
,使得任意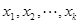
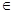
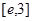 (
(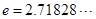 是自然对数的底数)都有
是自然对数的底数)都有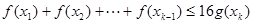 成立;
成立;
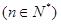 .
.