题目内容
已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若任取 ,求函数
,求函数 在
在 上是增函数的概率.
上是增函数的概率.
(Ⅰ)函数 的单调递增区间分别为
的单调递增区间分别为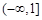 和
和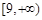 ;(Ⅱ)函数
;(Ⅱ)函数 在
在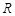 上是增函数的概率为
上是增函数的概率为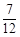 .
.
解析试题分析:(Ⅰ)求函数 的单调递增区间,首先将
的单调递增区间,首先将 代入,我们易求出函数的解析式,从而求出函数的导函数后,令导函数的函数值大于等于0,由此构造关于
代入,我们易求出函数的解析式,从而求出函数的导函数后,令导函数的函数值大于等于0,由此构造关于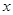 的不等式,解不等式即可得到函数
的不等式,解不等式即可得到函数 的单调递增区间;(Ⅱ)求函数
的单调递增区间;(Ⅱ)求函数 在
在 上是增函数的概率,这是一个几何概型问题,我们可以先画出
上是增函数的概率,这是一个几何概型问题,我们可以先画出 ,对应的平面区域的面积,然后再求出满足条件函数
,对应的平面区域的面积,然后再求出满足条件函数 在
在 上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
试题解析:(1)当 时,
时, ,
,
令 ,
, ,解得
,解得 或
或 ,
,
故函数 的单调递增区间分别为
的单调递增区间分别为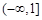 和
和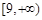
(2)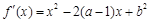
若函数 在
在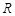 上是增函数,则对于任意
上是增函数,则对于任意 ,
,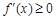 恒成立.
恒成立.
所以,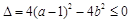 ,即
,即 8分
8分
设“ 在
在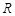 上是增函数”为事件
上是增函数”为事件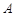 ,则事件
,则事件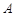 对应的区域为
对应的区域为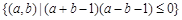
全部试验结果构成的区域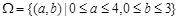 ,
,
所以,
故函数 在
在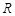 上是增函数的概率为
上是增函数的概率为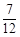
考点:利用导数研究函数的单调性;几何概型;概率的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 .
. 在(0,+∞)内的极值;
在(0,+∞)内的极值; ,
, ,且
,且 形成的平面区域的面积.
形成的平面区域的面积. .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. =
= 。
。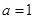 时,求函数
时,求函数 上的最小值;
上的最小值;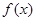 =
=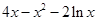 ,
,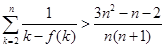 (
(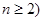 ),参考数据:
),参考数据: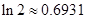 。(13分)
。(13分) ,如果函数
,如果函数 恰有两个不同的极值点
恰有两个不同的极值点 ,
, ,且
,且 .
. ;(Ⅱ)求
;(Ⅱ)求 的最小值,并指出此时
的最小值,并指出此时 的值.
的值. .
. 垂直,求
垂直,求 的值;
的值; .
. 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 ),
), (单位:弧度).
(单位:弧度).
 的函数;
的函数; 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t); ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值.

 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.