题目内容
已知函数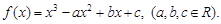 .
.
若函数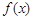 在
在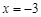 和
和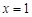 处取得极值,试求
处取得极值,试求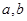 的值;
的值;
在(1)的条件下,当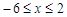 时,
时,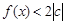 恒成立,求c的取值范围.
恒成立,求c的取值范围.
(1) (2)
(2)
解析试题分析:解:(1) 1分
1分
∵函数 在
在 和
和 处取得极值,∴
处取得极值,∴ 是方程
是方程 的两根.
的两根.
 3分
3分
(2) 由(1)知, 4分
4分
当x变化时, 的变化情况如下表:
的变化情况如下表:
而






+ 0 
0 + 
↗ 极大值 
↘ 极小值 
↗  ,
, ,
,  时,
时, 的最大值是
的最大值是 7分
7分
要使 恒成立,只要
恒成立,只要 即可,
即可,
当 时,
时, ;当
;当 时,
时,
 ,此即为c的取值范围
,此即为c的取值范围 10分
10分
考点:导数的运用
点评:主要是考查了导数判定函数单调性以及函数的极值和最值的运用,属于中档题。

练习册系列答案
相关题目
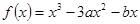 ,其中
,其中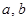 为实数.
为实数.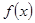 在
在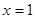 处取得的极值为
处取得的极值为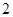 ,求
,求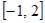 上为减函数,且
上为减函数,且 ,求
,求 的取值范围.
的取值范围.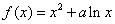
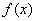 +
+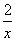 在
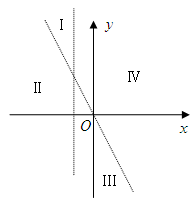
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.  ;
;
 在
在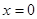 处取极值,求
处取极值,求 的值;
的值;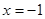 和
和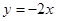 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若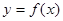 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的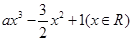 ,其中a>0,
,其中a>0, 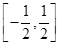 上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。 ,其中
,其中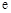 为自然对数的底数.
为自然对数的底数.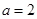 时,求曲线
时,求曲线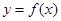 在
在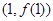 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;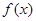 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为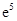 ,求
,求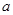 的
的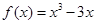
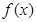 的单调区间;(2)求
的单调区间;(2)求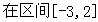 上的最小值.
上的最小值.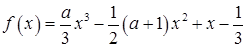 (
(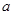
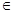 R).
R).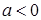 ,求函数
,求函数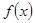 的极值;
的极值;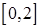 上有两个零点,若存在,求出
上有两个零点,若存在,求出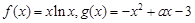 .
.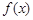 在
在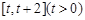 上的最小值;
上的最小值;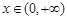 ,
,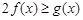 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.