题目内容
2.直线y=x被圆(x-1)2+y2=1所截得的弦长为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 找出圆心坐标与半径r,利用点到直线的距离公式求出圆心到直线的距离d,利用垂径定理及勾股定理求出弦长即可.
解答 解:由圆的方程得:圆心坐标为(1,0),半径r=1,
∵圆心到直线x-y=0的距离d=$\frac{1}{\sqrt{2}}$,
∴直线被圆截得的弦长为2$\sqrt{1-\frac{1}{2}}$=$\sqrt{2}$.
故选C.
点评 此题考查了直线与圆相交的性质,涉及的知识有:点到直线的距离公式,垂径定理,以及勾股定理,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.点P(0,1)到双曲线$\frac{y^2}{4}-{x^2}=1$渐近线的距离是( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 5 |
17.计算lg4+lg25=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 10 |
7.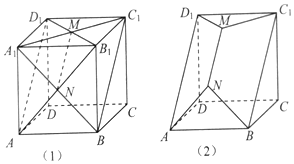 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
 如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )
如图(1),把棱长为1的正方体沿平面AB1D1和平面A1BC1截去部分后,得到如图(2)所示几何体,该几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{17}{24}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
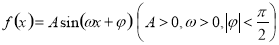 的图像过点
的图像过点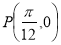 ,图像上与
,图像上与
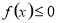 的取值范围
的取值范围 的值为
的值为 B.
B. C.
C. D.
D.