题目内容
已知圆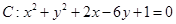 ,直线
,直线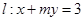 .
.
(Ⅰ)若 与
与 相切,求
相切,求 的值;
的值;
(Ⅱ)是否存在 值,使得
值,使得 与
与 相交于
相交于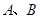 两点,且
两点,且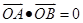 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.
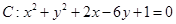 ,直线
,直线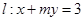 .
.(Ⅰ)若
 与
与 相切,求
相切,求 的值;
的值;(Ⅱ)是否存在
 值,使得
值,使得 与
与 相交于
相交于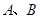 两点,且
两点,且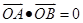 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.(Ⅰ) (Ⅱ)m=9±2
(Ⅱ)m=9±2
 (Ⅱ)m=9±2
(Ⅱ)m=9±2
试题分析:(Ⅰ)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),半径为 r = 3, 2分
若 l与C相切,则得
 =3,
=3,∴(3m-4)2=9(1+m2),∴m =
 . 5分
. 5分(Ⅱ)假设存在m满足题意。
由
 ,消去x得
,消去x得(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,得m>
 , 8分
, 8分设A(x1,y1),B(x2,y2),则y1+y2=
 ,y1y2=
,y1y2= .
.
 OA·OB=x1x2+y1y2
OA·OB=x1x2+y1y2=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·
 +(m2+1)·
+(m2+1)·
=25-
 =0 10分
=0 10分24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2
 ,适合m>
,适合m> ,
,∴存在m=9±2
 符合要求.
符合要求.点评:直线与圆相切,一般用圆心到直线的距离等于圆的半径,本题直线与圆相交联立方程利用韦达定理可得到焦点坐标与方程的关系,进而可将向量坐标化化简

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
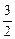 ,1+
,1+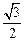 ),求直线l的方程;
),求直线l的方程;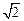 =0,P为圆M上任一点,求
=0,P为圆M上任一点,求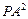 +
+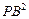 +
+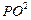 的最值.
的最值.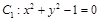 和
和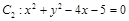 的位置关系是( )
的位置关系是( ) 相内切,且过点A(4,0),则这个动圆圆心的轨迹方程是_______________.
相内切,且过点A(4,0),则这个动圆圆心的轨迹方程是_______________.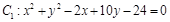 与
与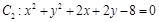 公共弦的长为 .
公共弦的长为 .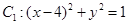 ,圆
,圆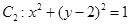 ,动点
,动点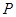 到圆
到圆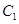 ,
,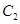 上点的距离的最小值相等.
上点的距离的最小值相等.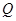 ,使得点
,使得点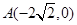 的距离减去点
的距离减去点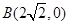 的距离的差为
的距离的差为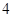 ,如果存在求出
,如果存在求出