题目内容
直线
与椭圆
相切，则t= ．
【答案】分析：由直线
与椭圆C：
相切转化为
只有一组解，即2x2-10tx+25（t2-1）=0只有一个解，从而有△=0，求解即可．
解答：解：直线
与椭圆C：
相切
只有一组解
即2x2-10tx+25t2-25=0只有一个根
△=100t2-200（t2-1）=0
解可得 t=
故答案为：
点评：本题主要考查了直线与椭圆相切的位置关系，处理的方法是把直线与椭圆方程联立，转化为方程只有一个解来求解．
与椭圆C：相切转化为只有一组解，即2x2-10tx+25（t2-1）=0只有一个解，从而有△=0，求解即可．解答：解：直线
与椭圆C：相切只有一组解即2x2-10tx+25t2-25=0只有一个根
△=100t2-200（t2-1）=0
解可得 t=
故答案为：
点评：本题主要考查了直线与椭圆相切的位置关系，处理的方法是把直线与椭圆方程联立，转化为方程只有一个解来求解．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知F是椭圆
与椭圆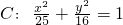
相切，则t=________．
的左焦点，A是椭圆短轴上的一个顶点，椭圆的离心率为
，点B在x轴上，AB⊥AF，A、B、F三点确定的圆C恰好与直线
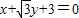相切．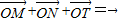
，如果存在，则求点T的坐标；如果不存在，请说明理由．