题目内容
直线l:| x |
| 5 |
| y |
| 4 |
| x2 |
| 25 |
| y2 |
| 16 |
分析:由直线l:
+
=t与椭圆C:
+
=1相切转化为
只有一组解,即2x2-10tx+25(t2-1)=0只有一个解,从而有△=0,求解即可.
| x |
| 5 |
| y |
| 4 |
| x2 |
| 25 |
| y2 |
| 16 |
|
解答:解:直线l:
+
=t与椭圆C:
+
=1相切
只有一组解
即2x2-10tx+25t2-25=0只有一个根
△=100t2-200(t2-1)=0
解可得 t=±
故答案为:±
| x |
| 5 |
| y |
| 4 |
| x2 |
| 25 |
| y2 |
| 16 |
|
即2x2-10tx+25t2-25=0只有一个根
△=100t2-200(t2-1)=0
解可得 t=±
| 2 |
故答案为:±
| 2 |
点评:本题主要考查了直线与椭圆相切的位置关系,处理的方法是把直线与椭圆方程联立,转化为方程只有一个解来求解.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

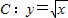 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为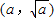 ,x1=b,0<b<a.
,x1=b,0<b<a.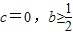 时,求证:
时,求证: .
. 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为 ,x1=b,0<b<a.
,x1=b,0<b<a. 时,求证:
时,求证: .
.