题目内容
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设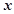 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求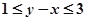 的概率;
的概率;
(Ⅱ)若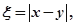 求随机变量
求随机变量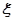 的分布列和数学期望。
的分布列和数学期望。
(Ⅰ)
(Ⅱ) ,分布列为
,分布列为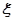
0 2 4 



解析试题分析:依题意知,掷一次骰子,球被放入甲盒、乙盒的概率分别为 2分
2分
(Ⅰ)若 则只能有
则只能有 即在4次掷骰子中,有1次在甲盒中放球,有3次在乙盒中放球,因此所求概率
即在4次掷骰子中,有1次在甲盒中放球,有3次在乙盒中放球,因此所求概率 ……5分
……5分
(Ⅱ)由于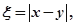 所以
所以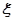 的可能取值有0,2,4…6分
的可能取值有0,2,4…6分

 9分
9分
所以随机变量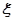 的分布列为:
的分布列为:
故随机变量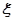
0 2 4 



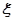 的数学期望为
的数学期望为 12分
12分
考点:独立重复试验与分布列
点评:在n次独立重复试验中,每一次事件A发生的概率为 ,则n次试验中有
,则n次试验中有 次发生的概率为
次发生的概率为 ,求分布列的步骤:找到随机变量可以取得值,求出各随机变量对应的概率,汇总成分布列
,求分布列的步骤:找到随机变量可以取得值,求出各随机变量对应的概率,汇总成分布列

练习册系列答案
相关题目
 .
.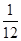 ,
,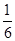 ,
,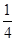 ,
,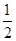 .游戏规则如下:
.游戏规则如下: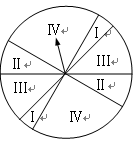
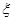 .
.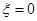 的概率;
的概率; 位学生,每次活动均需该系
位学生,每次活动均需该系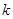 位学生参加(
位学生参加(
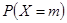 取得最大值的整数
取得最大值的整数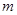 .
.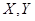 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记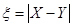 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望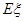 .
. ,乙每次击中目标的概率为
,乙每次击中目标的概率为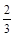
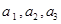 ,女生2名,记为
,女生2名,记为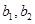 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛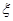 的概率密度函数
的概率密度函数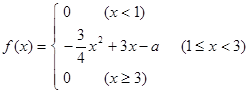 ,
, 的值,并画出
的值,并画出
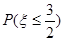 .
.
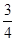 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有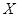 名获得优秀,求
名获得优秀,求