题目内容
下图是某游戏中使用的材质均匀的圆形转盘，其中Ⅰ，Ⅱ，Ⅲ，Ⅳ部分的面积各占转盘面积的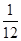
，
，
，
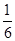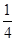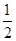．游戏规则如下：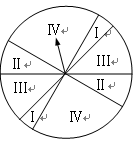
① 当指针指到Ⅰ，Ⅱ， Ⅲ，Ⅳ部分时，分别获得积分100分，40分，10分，0分；
② （ⅰ）若参加该游戏转一次转盘获得的积分不是40分，则按①获得相应的积分，游戏结束；
（ⅱ）若参加该游戏转一次获得的积分是40分，则用抛一枚质地均匀的硬币的方法来决定是否继续游戏．正面向上时，游戏结束；反面向上时，再转一次转盘，若再转一次的积分不高于40分，则最终积分为0分，否则最终积分为100分，游戏结束．
设某人参加该游戏一次所获积分为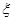
．
（1）求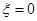
的概率；
（2）求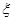的概率分布及数学期望．
（1）83:144
（2）
的概率分布为：0 10 40 100 
（分）
解析试题分析：解：（1）事件“
”包含：“首次积分为0分”和“首次积分为40分
后再转一次的积分不高于40分”，且两者互斥，
所以
； 4分
（2）的所有可能取值为0，10，40，100，
由（1）知
，
又
，
，
，
所以的概率分布为：
因此，0 10 40 100 
（分）． 10分
考点：独立事件的概率和期望
点评：主要是考查了独立事件的概率公式，以及分布列的求解，属于中档题。
练习册系列答案
相关题目
人，每人回答一个问题，答对者为本队赢得一分，答错得零分。假设甲队中每人答对的概率均为
，乙队中
且各人正确与否相互之间没有影响.用
表示甲队的总得分.
表示“甲、乙两个队总得分之和等于
表示“甲队总得分大于乙队总得分”这一事件，求
。某普通高中共有教师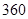
人，分为三个批次参加研修培训，在三个批次中男、女教师人数如下表所示：
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 |  |  |  |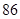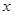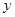
| 男教师 |  |  |  |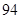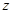
已知在全体教师中随机抽取1名，抽到第二、三批次中女教师的概率分别是
、
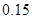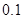．（Ⅰ）求
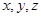的值；（Ⅱ）为了调查研修效果，现从三个批次中按
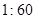的比例抽取教师进行问卷调查，三个批次被选取的人数分别是多少？（Ⅲ）若从（Ⅱ）中选取的教师中随机选出两名教师进行访谈，求参加访谈的两名教师“分别来自两个批次”的概率．
、
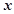分别表示甲、乙盒子中球的个数。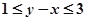
的概率；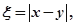
求随机变量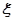
的分布列和数学期望。
，乙队每人答对的概率都是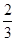
．设每人回答正确与否相互之间没有影响，用
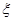表示甲队总得分．