题目内容
在平面直角坐标系 中,已知圆
中,已知圆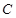 经过点
经过点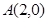 和点
和点 ,且圆心
,且圆心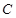 在直线
在直线 上,过点
上,过点 且斜率为
且斜率为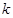 的直线与圆
的直线与圆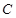 相交于不同的两点
相交于不同的两点 .
.
求圆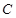 的方程, 同时求出
的方程, 同时求出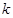 的取值范围.
的取值范围.
 中,已知圆
中,已知圆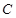 经过点
经过点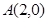 和点
和点 ,且圆心
,且圆心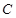 在直线
在直线 上,过点
上,过点 且斜率为
且斜率为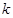 的直线与圆
的直线与圆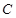 相交于不同的两点
相交于不同的两点 .
.求圆
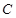 的方程, 同时求出
的方程, 同时求出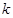 的取值范围.
的取值范围.(1)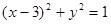 ;(2)
;(2)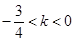
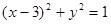 ;(2)
;(2)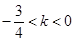
根据圆的几何性质可确定圆心弦AB的垂直平分线与直线x-y-3=0的交点,然后再求出半径.再利用直线与圆相交的充要条件是圆心到直线的距离小于半径,建立关于k的不等式,解出k的取值范围.
方法一:AB的中垂线方程为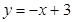 ………… 2分
………… 2分
联立方程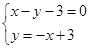 解得圆心坐标
解得圆心坐标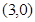 …… 5分
…… 5分
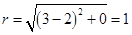 …………………………………… 6分
…………………………………… 6分
故圆的方程为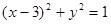 ………………………… 8分
………………………… 8分
方法2:设圆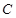 的方程为
的方程为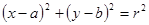 , ………… 2分
, ………… 2分
依题意得:
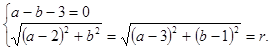 …… 5分,得
…… 5分,得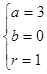 ………… 7分
………… 7分
故圆的方程为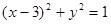 ………………………………………… 8分
………………………………………… 8分
方法一 由直线 与圆相交,得圆心C到直线的距离小于半径
与圆相交,得圆心C到直线的距离小于半径
∴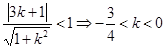 …………………………………… 14分
…………………………………… 14分
方法二:联立方程组
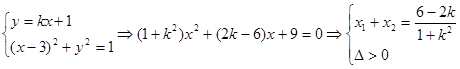
由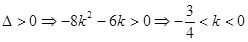 ………………………… 14分
………………………… 14分
方法一:AB的中垂线方程为
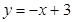 ………… 2分
………… 2分 联立方程
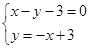 解得圆心坐标
解得圆心坐标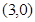 …… 5分
…… 5分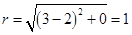 …………………………………… 6分
…………………………………… 6分故圆的方程为
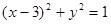 ………………………… 8分
………………………… 8分方法2:设圆
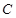 的方程为
的方程为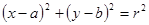 , ………… 2分
, ………… 2分依题意得:
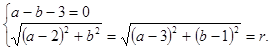 …… 5分,得
…… 5分,得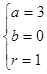 ………… 7分
………… 7分故圆的方程为
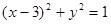 ………………………………………… 8分
………………………………………… 8分方法一 由直线
 与圆相交,得圆心C到直线的距离小于半径
与圆相交,得圆心C到直线的距离小于半径∴
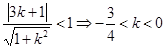 …………………………………… 14分
…………………………………… 14分方法二:联立方程组
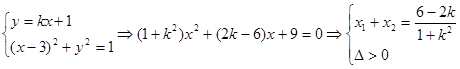
由
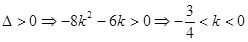 ………………………… 14分
………………………… 14分
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
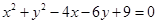 及直
及直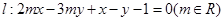
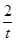 )(t∈R , t≠ 0)为圆心的圆与
)(t∈R , t≠ 0)为圆心的圆与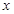 轴交于点O, A,
轴交于点O, A,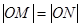 ,求圆C的方程.
,求圆C的方程.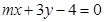 与圆
与圆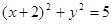 相交于
相交于 、
、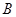 两点,若
两点,若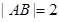 ,则实数
,则实数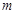 的值为( )
的值为( )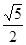
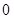 或
或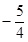

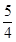
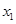 、
、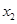 是关于x的方程
是关于x的方程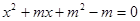 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点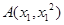 ,
,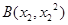 的直线与圆
的直线与圆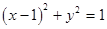 的位置关系是( )
的位置关系是( )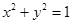 上的点到直线
上的点到直线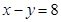 的距离的最小值
的距离的最小值 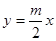 与圆
与圆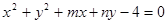 交于
交于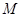 、
、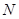 两点,且
两点,且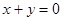 对称,则弦
对称,则弦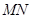 的长为( )
的长为( ) 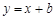 交圆
交圆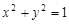 于A、B两点,且
于A、B两点,且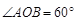 (O为原点),则实数
(O为原点),则实数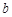 的值为 .
的值为 .